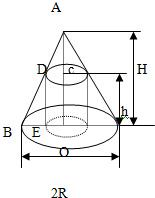
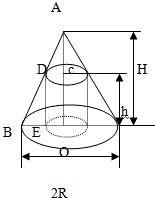
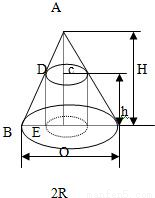
摘要：化为图形是椭圆已知圆锥体的底面半径为R.高为H求内接于这个圆锥体并且体积最大的圆柱体的高h A D c H h B E O 2R 解:设圆柱体半径为r高为h由△ACD∽△AOB得由此得圆柱体体积由题意.H＞h＞0.利用均值不等式.有(注:原“解一 对h求导由驻点解得)五．解一:当>1时.解二:六． A M P X O N B 如图:已知锐角∠AOB=2α内有动点P.PM⊥OA.PN⊥OB.且四边形PMON的面积等于常数c2今以O为极点.∠AOB的角平分线OX为极轴.求动点P的轨迹的极坐标方程.并说明它表示什么曲线解:设P的极点坐标为∴∠POM=α-θ.∠NOM=α+θ.OM=ρcos,PM=ρsin,ON=ρcos,PN=ρsin,四边形PMON的面积这个方程表示双曲线由题意.动点P的轨迹是双曲线右面一支在∠AOB内的一部分 七．已知空间四边形ABCD中AB=BC.CD=DA.M.N.P.Q分别是边AB.BC.CD.DA的中点求证MNPQ是一个矩形

网址：http://m.1010jiajiao.com/timu_id_5364[举报]