摘要：AD⊥DE.在第(19)图2中.因A-DE-B是直二面角.AD⊥DE,故AD⊥底面DBCE.从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线.
网址：http://m.1010jiajiao.com/timu_id_531349[举报]
请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分.
（本小题满分10分）选修4—1：几何证明选讲
如图，⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．
（Ⅰ）求证：AD∥EC；
（Ⅱ）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长．
查看习题详情和答案>>
请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分.
（本小题满分10分）选修4—1：几何证明选讲
如图，⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．
（Ⅰ）求证：AD∥EC；
（Ⅱ）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长．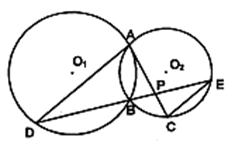
（请考生在第22、23两题中任选一题作
答，如果多做。则按所做的第一题记分．
（本小题满分10分）选修4－1：几何证明选讲
如图：AB是⊙O的直径，G是AB延长线上的一点，GCD是⊙O的割线，过点G作AG的垂线，交直线AC于点E，交直线AD于点F，过点G作⊙O的切线，切点为H．求证：
（Ⅰ）C、D、F、E四点共圆；
（Ⅱ）GH2＝GE·GF．
如图，边长为a的正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形，现给出下列命题，其中正确的命题有