摘要:因为..有.又..所以..从而..
网址:http://m.1010jiajiao.com/timu_id_528937[举报]
已知m>1,直线 ,椭圆C:
,椭圆C: ,
, 、
、 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.
(Ⅰ)当直线过右焦点 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A
 、△B
、△B
 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.[
【解析】第一问中因为直线 经过点
经过点 (
( ,0),所以
,0),所以 =
= ,得
,得 .又因为m>1,所以
.又因为m>1,所以 ,故直线的方程为
,故直线的方程为
第二问中设 ,由
,由 ,消去x,得
,消去x,得 ,
,
则由 ,知
,知 <8,且有
<8,且有
由题意知O为
 的中点.由
的中点.由 可知
可知 从而
从而 ,设M是GH的中点,则M(
,设M是GH的中点,则M( ).
).
由题意可知,2|MO|<|GH|,得到范围
查看习题详情和答案>>
已知函数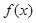 定义域为R,且
定义域为R,且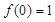 ,对任意
,对任意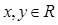 恒有
恒有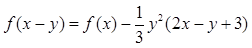 ,
,
(1)求函数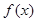 的表达式;
的表达式;
(2)若方程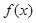 =
=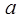 有三个实数解,求实数
有三个实数解,求实数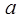 的取值范围;
的取值范围;
【解析】第一问中,利用因为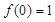 ,对任意
,对任意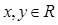 恒有
恒有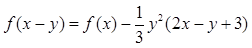 ,
,
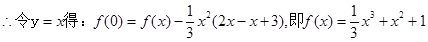
第二问中,因为方程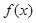 =
=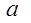 有三个实数解,所以
有三个实数解,所以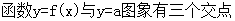
又因为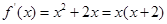 当
当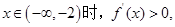
 ;
;
当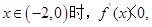
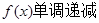 从而得到范围。
从而得到范围。
解:(1)因为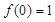 ,对任意
,对任意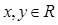 恒有
恒有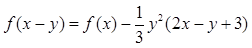 ,
,
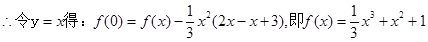
(2)因为方程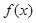 =
=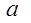 有三个实数解,所以
有三个实数解,所以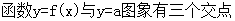
又因为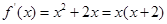 ,当
,当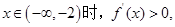
 ;
;
当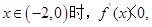
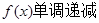 ;当
;当

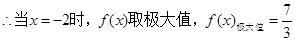 ,
,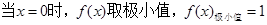
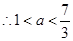
查看习题详情和答案>>
请阅读下列材料:对命题“若两个正实数a1,a2满足a12+a22=1,那么a1+a2≤
.”证明如下:构造函数f(x)=(x-a1)2+(x-a2)2,因为对一切实数x,恒有f(x)≥0,又f(x)=2x2-2(a1+a2)x+1,从而得4(a1+a2)2-8≤0,所以a1+a2≤
.根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你可以构造函数g(x)= ,进一步能得到的结论为 .(不必证明)
查看习题详情和答案>>
| 2 |
| 2 |
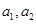 满足
满足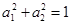 ,那么
,那么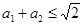 。”
。”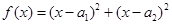 ,因为对一切实数
,因为对一切实数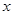 ,恒有
,恒有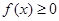 ,
,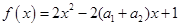 ,从而得
,从而得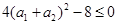 ,所以
,所以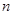 个正实数满足
个正实数满足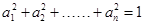 时,你可以构造函数
时,你可以构造函数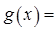 _______ ,进一步能得到的结论为
______________ (不必证明).
_______ ,进一步能得到的结论为
______________ (不必证明).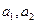 满足
满足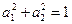 ,那么
,那么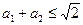 。”
。”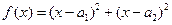 ,因为对一切实数
,因为对一切实数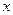 ,恒有
,恒有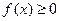 ,
,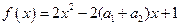 ,从而得
,从而得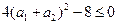 ,所以
,所以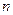 个正实数满足
个正实数满足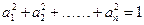 时,你可以构造函数
时,你可以构造函数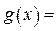 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).