网址:http://m.1010jiajiao.com/timu_id_526493[举报]
一、选择题:1-5 :A D B D C 6-10: C C C
D B 11-12: B B 学科网
学科网
二、填空题: 13,  14. 3 15.
14. 3 15. 16. (1,2),(3,402)
16. (1,2),(3,402) 学科网
学科网
三、解答题
三、解答题(本大题共6小题,共70分)
17.(12分)
解:(1)
 ∥
∥

 2分
2分
 4分
4分
又 为锐角
为锐角 

 6分
6分
(Ⅱ)
 由
由  得
得 
又 代入上式得:
代入上式得: (当且仅当
(当且仅当 时等号成立。) 9分
时等号成立。) 9分

 (当且仅当
(当且仅当 时等号成立。) 11分
时等号成立。) 11分

 的面积
的面积 的取值范围为.
的取值范围为. 12分
12分
18.(12分)
 解法一:
解法一:
(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 ,
, .
.
 ,
, .
.
 ,
, 平面
平面 .
.
 平面
平面 ,
, .
.
(Ⅱ) ,
, ,
,
 .
.
又 ,
, .
.
 又
又 ,即
,即 ,且
,且 ,
,
 平面
平面 .
.
取 中点
中点 .连结
.连结 .
.
 ,
, .
.
 是
是 在平面
在平面 内的射影,
内的射影,
 .
.
 是二面角
是二面角 的平面角.
的平面角.
在 中,
中, ,
, ,
, ,
,

 .
. 二面角
二面角 的余弦值为
的余弦值为
(Ⅲ)由(Ⅰ)知 平面
平面 ,
,
 平面
平面 平面
平面 .
.
过 作
作 ,垂足为
,垂足为 .
.
 平面
平面 平面
平面 ,
,
 平面
平面 .
.
 的长即为点
的长即为点 到平面
到平面 的距离.
的距离.
由(Ⅰ)知 ,又
,又 ,且
,且 ,
,
 平面
平面 .
. 平面
平面 ,
,
 .
.
在 中,
中, ,
, ,
, .
. .
.
 点
点 到平面
到平面 的距离为
的距离为 .
.
解法二:
(Ⅰ) ,
, ,
, .
.
又 ,
, .
.
 ,
, 平面
平面 .
.
 平面
平面 ,
, .
.
(Ⅱ)如图,以 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.
则 .设
.设 .
.
 ,
, ,
, .
.
取 中点
中点 ,连结
,连结 .
.
 ,
, ,
,
 ,
, .
.
 是二面角
是二面角 的平面角.
的平面角.
 ,
, ,
, ,
,
 .
. 二面角
二面角 的余弦值为
的余弦值为 .
.
(Ⅲ) ,
,
 在平面
在平面 内的射影为正
内的射影为正 的中心
的中心 ,且
,且 的长为点
的长为点 到平面
到平面 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系 .
.
 ,
, 点
点 的坐标为
的坐标为 .
.
 .
. 点
点 到平面
到平面 的距离为
的距离为 .
.
19.(12分)
解:(Ⅰ)由条件得 ,又
,又 时,
时, ,
,
故数列 构成首项为1,公式为
构成首项为1,公式为 的等比数列.从而
的等比数列.从而 ,即
,即 .
.
(Ⅱ)由 得
得 ,
,
 ,
,
两式相减得 :  ,
所以
,
所以  .
.
(Ⅲ)由 得
得

所以
 .
.
20.(12分)
解:(Ⅰ)①当0<t 10时,V(t)=(-t2+14t-40)
10时,V(t)=(-t2+14t-40)
化简得t2-14t+40>0,
解得t<4,或t>10,又0<t 10,故0<t<4.
10,故0<t<4.
②当10<t 12时,V(t)=4(t-10)(3t-41)+50<50,
12时,V(t)=4(t-10)(3t-41)+50<50,
化简得(t-10)(3t-41)<0,
解得10<t< ,又10<t
,又10<t 12,故 10<t
12,故 10<t 12.
12.
综合得0<t<4,或10<t 12,
12,
故知枯水期为1月,2月, 3月,4月,11月,12月共6个月.
(Ⅱ)由(Ⅰ)知:V(t)的最大值只能在(4,10)内达到.
由V′(t)=
令V′(t)=0,解得t=8(t=-2舍去).
当t变化时,V′(t) 与V (t)的变化情况如下表:
t
(4,8)
8
(8,10)
V′(t)
+
0
-
V(t)

极大值

由上表,V(t)在t=8时取得最大值V(8)=8e2+50-108.32(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
21.(12分)
解:(Ⅰ)由题意得直线 的方程为
的方程为 .
.
因为四边形 为菱形,所以
为菱形,所以 .
.
于是可设直线 的方程为
的方程为 .
.
由 得
得 .
.
因为 在椭圆上,
在椭圆上,
所以 ,解得
,解得 .
.
设 两点坐标分别为
两点坐标分别为 ,
,
则 ,
, ,
, ,
, .
.
所以 .
.
所以 的中点坐标为
的中点坐标为 .
.
由四边形 为菱形可知,点
为菱形可知,点 在直线
在直线 上,
上,
所以 ,解得
,解得 .
.
所以直线 的方程为
的方程为 ,即
,即 .
.
(Ⅱ)因为四边形 为菱形,且
为菱形,且 ,
,
所以 .
.
所以菱形 的面积
的面积 .
.
由(Ⅰ)可得 ,
,
所以 .
.
所以当 时,菱形
时,菱形 的面积取得最大值
的面积取得最大值 .
.
22.(10分)解:从⊙O外一点P向圆引两条切线PA、PB和割线PCD。从A点作弦AE平行于CD,连结BE交CD于F。求证:BE平分CD.
 【分析1】构造两个全等△.
【分析1】构造两个全等△.
连结ED、AC、AF。
CF=DF←△ACF≌△EDF←
←
←∠PAB=∠AEB=∠PFB
【分析2】利用圆中的等量关系。连结OF、OP、OB.

←∠PFB=∠POB←
←
23.(10分)解:(Ⅰ) 是圆,
是圆, 是直线.
是直线.
 的普通方程为
的普通方程为 ,圆心
,圆心 ,半径
,半径 .
.
 的普通方程为
的普通方程为 .
.
因为圆心 到直线
到直线 的距离为
的距离为 ,所以
,所以 与
与 只有一个公共点.
只有一个公共点.
(Ⅱ)压缩后的参数方程分别为
 :
: (
( 为参数);
为参数);  :
: (t为参数).
(t为参数).
化为普通方程为: :
: ,
, :
: ,
,
联立消元得 ,其判别式
,其判别式 ,
,
所以压缩后的直线 与椭圆
与椭圆 仍然只有一个公共点,和
仍然只有一个公共点,和 与
与 公共点个数相同.
公共点个数相同.
24.(10分)解:
(Ⅰ)
图像如下:


(Ⅱ)不等式
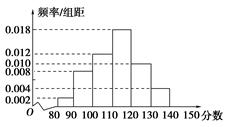
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
男生
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K2=
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率. 查看习题详情和答案>>

男生
女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K2=
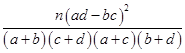 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.
