网址:http://m.1010jiajiao.com/timu_id_514880[举报]
一、选择题:本大题共12小题,每小题5分,共60分.
1.A 2.C 3.C 4.A 5.C 6.B 7.D 8.C 9.D 10.D 11.B 12.D
二、填空题:本大题共4小题,每小题4分,共16分.
13.--数学理科.files/image181.gif) 14.±2 15.
14.±2 15.--数学理科.files/image183.gif) 16.40
16.40
三、解答题:本大题共6小题,共74分解答应写出文字说明,证明过程或演算步骤.
17.解:--数学理科.files/image185.gif)
--数学理科.files/image187.gif)
--数学理科.files/image189.gif) ,联合
,联合--数学理科.files/image190.gif)
得--数学理科.files/image192.gif) ,即
,即--数学理科.files/image194.gif)
当--数学理科.files/image196.gif) 时,
时,--数学理科.files/image198.gif)
当--数学理科.files/image200.gif) 时,
时,--数学理科.files/image202.gif)
∴当--数学理科.files/image204.gif) 时,
时,--数学理科.files/image206.gif)
当--数学理科.files/image208.gif) 时,
时,--数学理科.files/image210.gif)
--数学理科.files/image212.gif)
18.解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1.
(1)连结AC1,AB1.
由直三棱柱的性质得AA1⊥平面A1B
所以AA1⊥A1B1,则四边形ABB
由矩形性质得AB1过A1B的中点M.
在△AB
又AC1--数学理科.files/image012.gif) 平面ACC
平面ACC--数学理科.files/image215.gif) 平面ACC
平面ACC
所以MN//平面ACC
(2)因为BC⊥平面ACC--数学理科.files/image012.gif) 平面ACC
平面ACC
所以BC⊥AC1.
在正方形ACC
又因为BC∩A
由MN//AC1,得MN⊥平面A1BC.
(3)由题意CB,CA,CC1两两垂直,故可以C为的点,
CB,CA,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
又AC = BC = CC1 = a,
则--数学理科.files/image217.gif)
则AB中点E的坐标为--数学理科.files/image219.gif) ,
,
--数学理科.files/image221.gif) 为平面AA1B的法向量.
为平面AA1B的法向量.
又AC1⊥平面A1BC,故--数学理科.files/image223.gif) 为平面A1BC的法向量
为平面A1BC的法向量
设二面角A―A1B―C的大小为θ,
则--数学理科.files/image225.gif)
由题意可知,θ为锐角,所以θ= 60°,即二面角A―A1B―C为60°
19.解:(1)每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的.
所以恰好有两家煤矿必须整改的概率是
--数学理科.files/image227.gif) .
.
(2)由题设,必须整改的煤矿数--数学理科.files/image229.gif) 服从二项分布B(5,0.5).从而
服从二项分布B(5,0.5).从而--数学理科.files/image229.gif) 的数学期望是
的数学期望是
E--数学理科.files/image229.gif) =
=--数学理科.files/image231.gif) ,即平均有2.50家煤矿必须整改.
,即平均有2.50家煤矿必须整改.
(3)某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是--数学理科.files/image233.gif) ,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是
,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是--数学理科.files/image235.gif)
20.(1)依题意,点--数学理科.files/image237.gif) 的坐标为
的坐标为--数学理科.files/image239.gif) ,可设
,可设--数学理科.files/image241.gif) ,
,
直线--数学理科.files/image099.gif) 的方程为
的方程为--数学理科.files/image244.gif) ,与
,与--数学理科.files/image246.gif) 联立得
联立得--数学理科.files/image248.gif)
消去--数学理科.files/image250.gif) 得
得--数学理科.files/image252.gif) .
.
--数学理科.files/image253.gif) 由韦达定理得
由韦达定理得--数学理科.files/image255.gif) ,
,--数学理科.files/image257.gif) .
.
于是--数学理科.files/image259.gif) .
.
--数学理科.files/image261.gif)
--数学理科.files/image263.gif) ,
,
--数学理科.files/image265.gif) 当
当--数学理科.files/image267.gif) ,
,--数学理科.files/image269.gif) .
.
(2)假设满足条件的直线--数学理科.files/image271.gif) 存在,其方程为
存在,其方程为--数学理科.files/image273.gif) ,
,
设--数学理科.files/image275.gif) 的中点为
的中点为--数学理科.files/image277.gif) ,
,--数学理科.files/image271.gif) 与
与--数学理科.files/image275.gif) 为直径的圆相交于点
为直径的圆相交于点--数学理科.files/image281.gif) ,
,--数学理科.files/image283.gif) 的中点为
的中点为--数学理科.files/image285.gif) ,
,
--数学理科.files/image287.gif) 则
则--数学理科.files/image289.gif) ,
,--数学理科.files/image291.gif) 点的坐标为
点的坐标为--数学理科.files/image293.gif) .
.
--数学理科.files/image295.gif) ,
,
--数学理科.files/image297.gif) ,
,
--数学理科.files/image299.gif)
--数学理科.files/image301.gif)
--数学理科.files/image303.gif) ,
,
--数学理科.files/image305.gif)
--数学理科.files/image307.gif) .
.
令--数学理科.files/image309.gif) ,得
,得--数学理科.files/image311.gif) ,此时
,此时--数学理科.files/image313.gif) 为定值,故满足条件的直线
为定值,故满足条件的直线--数学理科.files/image271.gif) 存在,其方程为
存在,其方程为--数学理科.files/image316.gif) ,即抛物线的通径所在的直线.
,即抛物线的通径所在的直线.
21.解:(1)当--数学理科.files/image123.gif) 时,
时,--数学理科.files/image319.gif) ,
,
∵--数学理科.files/image321.gif)
--数学理科.files/image323.gif) ,∴
,∴--数学理科.files/image125.gif) 在
在--数学理科.files/image127.gif) 上是减函数.
上是减函数.
(2)∵--数学理科.files/image129.gif) 不等式
不等式--数学理科.files/image131.gif) 恒成立,即
恒成立,即--数学理科.files/image129.gif) 不等式
不等式--数学理科.files/image330.gif) 恒成立,
恒成立,
∴--数学理科.files/image129.gif) 不等式
不等式--数学理科.files/image333.gif) 恒成立. 当
恒成立. 当--数学理科.files/image335.gif) 时,
时,--数学理科.files/image129.gif)
--数学理科.files/image338.gif) 不恒成立;
不恒成立;
当--数学理科.files/image340.gif) 时,
时,--数学理科.files/image129.gif) 不等式
不等式--数学理科.files/image333.gif) 恒成立,即
恒成立,即--数学理科.files/image344.gif) ,∴
,∴--数学理科.files/image346.gif) .
.
当--数学理科.files/image348.gif) 时,
时,--数学理科.files/image129.gif) 不等式
不等式--数学理科.files/image351.gif) 不恒成立. 综上,
不恒成立. 综上,--数学理科.files/image133.gif) 的取值范围是
的取值范围是--数学理科.files/image354.gif) .
.
22.解:(1)∵ --数学理科.files/image143.gif) 的横坐标构成以
的横坐标构成以--数学理科.files/image147.gif) 为首项,
为首项,--数学理科.files/image149.gif) 为公差的等差数列
为公差的等差数列--数学理科.files/image151.gif)
∴ --数学理科.files/image358.gif) .
.
∵ --数学理科.files/image139.gif) 位于函数
位于函数--数学理科.files/image145.gif) 的图象上,
的图象上,
∴ --数学理科.files/image361.gif) ,
,
∴ 点--数学理科.files/image143.gif) 的坐标为
的坐标为--数学理科.files/image363.gif) .
.
(2)据题意可设抛物线--数学理科.files/image157.gif) 的方程为:
的方程为:--数学理科.files/image365.gif) ,
,
即--数学理科.files/image367.gif) .
.
∵ 抛物线--数学理科.files/image157.gif) 过点
过点--数学理科.files/image161.gif) (0,
(0,--数学理科.files/image369.gif) ),
),
∴ --数学理科.files/image371.gif) ,
,
∴ --数学理科.files/image373.gif) ∴
∴ --数学理科.files/image375.gif) .
.
∵ 过点--数学理科.files/image161.gif) 且与抛物线
且与抛物线--数学理科.files/image157.gif) 只有一个交点的直线即为以
只有一个交点的直线即为以--数学理科.files/image161.gif) 为切点的切线,
为切点的切线,
∴ --数学理科.files/image377.gif) .
.
∴ --数学理科.files/image379.gif) (
(--数学理科.files/image381.gif) ),
),
∴ --数学理科.files/image383.gif)
--数学理科.files/image385.gif)
∴ --数学理科.files/image387.gif) .
.
(3)∵ --数学理科.files/image389.gif)
--数学理科.files/image391.gif) ,
,
∴ --数学理科.files/image177.gif) 中的元素即为两个等差数列
中的元素即为两个等差数列--数学理科.files/image394.gif) 与
与--数学理科.files/image396.gif) 中的公共项,它们组成以
中的公共项,它们组成以--数学理科.files/image398.gif) 为首项,以
为首项,以--数学理科.files/image400.gif) 为公差的等差数列.
为公差的等差数列.
∵ --数学理科.files/image173.gif) ,且
,且--数学理科.files/image171.gif) 成等差数列,
成等差数列,--数学理科.files/image175.gif) 是
是--数学理科.files/image177.gif) 中的最大数,
中的最大数,
∴ --数学理科.files/image403.gif) ,其公差为
,其公差为--数学理科.files/image405.gif) .
.
--数学理科.files/image407.gif) 当
当--数学理科.files/image409.gif) 时,
时,--数学理科.files/image411.gif) ,
,
此时--数学理科.files/image413.gif) ∴ 不满足题意,舍去.
∴ 不满足题意,舍去.
--数学理科.files/image415.gif) 当
当--数学理科.files/image417.gif) 时,
时,--数学理科.files/image419.gif) ,
,
此时--数学理科.files/image421.gif) ,
,
∴ --数学理科.files/image423.gif) .
.
--数学理科.files/image425.gif) 当
当--数学理科.files/image427.gif) 时,
时,--数学理科.files/image429.gif) .
.
此时--数学理科.files/image431.gif) , 不满足题意,舍去.
, 不满足题意,舍去.
综上所述,所求通项为--数学理科.files/image423.gif) .
.
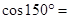 ( )
( )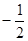 B.
B. C.
C.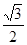 D.
D.
 =(
)
=(
) B.
B. C.
C. D.
D.