网址:http://m.1010jiajiao.com/timu_id_514706[举报]
一、选择题:本大题共12小题,每小题5分,共60分.
1.A 2.C 3.C 4.A 5.C 6.C 7.B 8.C 9.D 10.D 11.D 12.D
二、填空题:本大题共4小题,每小题4分,共16分.
13.--数学文科.files/image172.gif) 14.
14.--数学文科.files/image174.gif) 15.
15.--数学文科.files/image176.gif) 16.40
16.40
三、解答题:本大题共6小题,共74分解答应写出文字说明,证明过程或演算步骤.
17.解:--数学文科.files/image178.gif)
--数学文科.files/image180.gif)
--数学文科.files/image182.gif) ,联合
,联合--数学文科.files/image183.gif)
得--数学文科.files/image185.gif) ,即
,即--数学文科.files/image187.gif)
当--数学文科.files/image189.gif) 时,
时,--数学文科.files/image191.gif)
当--数学文科.files/image193.gif) 时,
时,--数学文科.files/image195.gif)
∴当--数学文科.files/image197.gif) 时,
时,--数学文科.files/image199.gif)
当--数学文科.files/image201.gif) 时,
时,--数学文科.files/image203.gif)
--数学文科.files/image205.gif)
18.解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1.
(1)连结AC1,AB1.
由直三棱柱的性质得AA1⊥平面A1B
由矩形性质得AB1过A1B的中点M.
在△AB
又AC1--数学文科.files/image012.gif) 平面ACC
平面ACC--数学文科.files/image208.gif) 平面ACC
平面ACC
所以MN//平面ACC
(2)因为BC⊥平面ACC--数学文科.files/image012.gif) 平面ACC
平面ACC
在正方形ACC
又因为BC∩A
--数学文科.files/image210.gif) 由MN//AC1,得MN⊥平面A1BC
由MN//AC1,得MN⊥平面A1BC
的元素一一对应.
因为S中点的总数为5×5=25(个),所以基本事侉总数为n=25
事件A包含的基本事件数共5个:
(1,5)、(2,4)、(3,3)、(4,2)、(5,1),
所以--数学文科.files/image212.gif)
(2)B与C不是互斥事件.因为事件B与C可以同时发生,如甲赢一次,乙赢两次的事件即符合题意
(3)这种游戏规则不公平.由 (Ⅰ)知和为偶数的基本事件数为13个:
(1,1)、(1,3)、(1,5)、(2,2)、(2,4)、(3,1)、(3,3)、(3,5)、(4,2)、(4,4)、(5,1)、 (5,3)、(5,5)
所以甲赢的概率为--数学文科.files/image214.gif) ,乙赢的概率为
,乙赢的概率为--数学文科.files/image216.gif) ,
,
所以这种游戏规则不公平.
20.(1)依题意,点--数学文科.files/image218.gif) 的坐标为
的坐标为--数学文科.files/image220.gif) ,可设
,可设--数学文科.files/image222.gif) ,
,
直线--数学文科.files/image090.gif) 的方程为
的方程为--数学文科.files/image225.gif) ,与
,与--数学文科.files/image227.gif) 联立得
联立得--数学文科.files/image229.gif)
消去--数学文科.files/image231.gif) 得
得--数学文科.files/image233.gif) .
.
--数学文科.files/image234.gif) 由韦达定理得
由韦达定理得--数学文科.files/image236.gif) ,
,--数学文科.files/image238.gif) .
.
于是--数学文科.files/image240.gif) .
.
--数学文科.files/image242.gif)
--数学文科.files/image244.gif) ,
,
--数学文科.files/image246.gif) 当
当--数学文科.files/image248.gif) ,
,--数学文科.files/image250.gif) .
.
(2)假设满足条件的直线--数学文科.files/image252.gif) 存在,其方程为
存在,其方程为--数学文科.files/image254.gif) ,
,
设--数学文科.files/image256.gif) 的中点为
的中点为--数学文科.files/image258.gif) ,
,--数学文科.files/image252.gif) 与
与--数学文科.files/image256.gif) 为直径的圆相交于点
为直径的圆相交于点--数学文科.files/image262.gif) ,
,--数学文科.files/image264.gif) 的中点为
的中点为--数学文科.files/image266.gif) ,
,
--数学文科.files/image268.gif) 则
则--数学文科.files/image270.gif) ,
,--数学文科.files/image272.gif) 点的坐标为
点的坐标为--数学文科.files/image274.gif) .
.
--数学文科.files/image276.gif) ,
,
--数学文科.files/image278.gif) ,
,
--数学文科.files/image280.gif)
--数学文科.files/image282.gif)
--数学文科.files/image284.gif) ,
,
--数学文科.files/image286.gif)
--数学文科.files/image288.gif) .
.
令--数学文科.files/image290.gif) ,得
,得--数学文科.files/image292.gif) ,此时
,此时--数学文科.files/image294.gif) 为定值,故满足条件的直线
为定值,故满足条件的直线--数学文科.files/image252.gif) 存在,其方程为
存在,其方程为--数学文科.files/image297.gif) ,即抛物线的通径所在的直线.
,即抛物线的通径所在的直线.
21.解:(1)当--数学文科.files/image114.gif) 时,
时,--数学文科.files/image300.gif) ,
,
∵--数学文科.files/image302.gif)
--数学文科.files/image304.gif) ,∴
,∴--数学文科.files/image116.gif) 在
在--数学文科.files/image118.gif) 上是减函数.
上是减函数.
(2)∵--数学文科.files/image120.gif) 不等式
不等式--数学文科.files/image122.gif) 恒成立,即
恒成立,即--数学文科.files/image120.gif) 不等式
不等式--数学文科.files/image311.gif) 恒成立,
恒成立,
∴--数学文科.files/image120.gif) 不等式
不等式--数学文科.files/image314.gif) 恒成立. 当
恒成立. 当--数学文科.files/image316.gif) 时,
时,--数学文科.files/image120.gif)
--数学文科.files/image319.gif) 不恒成立;
不恒成立;
当--数学文科.files/image321.gif) 时,
时,--数学文科.files/image120.gif) 不等式
不等式--数学文科.files/image314.gif) 恒成立,即
恒成立,即--数学文科.files/image325.gif) ,∴
,∴--数学文科.files/image327.gif) .
.
当--数学文科.files/image329.gif) 时,
时,--数学文科.files/image120.gif) 不等式
不等式--数学文科.files/image332.gif) 不恒成立. 综上,
不恒成立. 综上,--数学文科.files/image124.gif) 的取值范围是
的取值范围是--数学文科.files/image335.gif) .
.
22.解:(1)∵ --数学文科.files/image134.gif) 的横坐标构成以
的横坐标构成以--数学文科.files/image138.gif) 为首项,
为首项,--数学文科.files/image140.gif) 为公差的等差数列
为公差的等差数列--数学文科.files/image142.gif)
∴ --数学文科.files/image339.gif) .
.
∵ --数学文科.files/image130.gif) 位于函数
位于函数--数学文科.files/image136.gif) 的图象上,
的图象上,
∴ --数学文科.files/image342.gif) ,
,
∴ 点--数学文科.files/image134.gif) 的坐标为
的坐标为--数学文科.files/image344.gif) .
.
(2)据题意可设抛物线--数学文科.files/image148.gif) 的方程为:
的方程为:--数学文科.files/image346.gif) ,
,
即--数学文科.files/image348.gif) .
.
∵ 抛物线--数学文科.files/image148.gif) 过点
过点--数学文科.files/image152.gif) (0,
(0,--数学文科.files/image350.gif) ),
),
∴ --数学文科.files/image352.gif) ,
,
∴ --数学文科.files/image354.gif) ∴
∴ --数学文科.files/image356.gif) .
.
∵ 过点--数学文科.files/image152.gif) 且与抛物线
且与抛物线--数学文科.files/image148.gif) 只有一个交点的直线即为以
只有一个交点的直线即为以--数学文科.files/image152.gif) 为切点的切线,
为切点的切线,
∴ --数学文科.files/image358.gif) .
.
∴ --数学文科.files/image360.gif) (
(--数学文科.files/image362.gif) ),
),
∴ --数学文科.files/image364.gif)
--数学文科.files/image366.gif)
∴ --数学文科.files/image368.gif) .
.
(3)∵ --数学文科.files/image370.gif)
--数学文科.files/image372.gif) ,
,
∴ --数学文科.files/image168.gif) 中的元素即为两个等差数列
中的元素即为两个等差数列--数学文科.files/image375.gif) 与
与--数学文科.files/image377.gif) 中的公共项,它们组成以
中的公共项,它们组成以--数学文科.files/image379.gif) 为首项,以
为首项,以--数学文科.files/image381.gif) 为公差的等差数列.
为公差的等差数列.
∵ --数学文科.files/image164.gif) ,且
,且--数学文科.files/image162.gif) 成等差数列,
成等差数列,--数学文科.files/image166.gif) 是
是--数学文科.files/image168.gif) 中的最大数,
中的最大数,
∴ --数学文科.files/image384.gif) ,其公差为
,其公差为--数学文科.files/image386.gif) .
.
--数学文科.files/image388.gif) 当
当--数学文科.files/image390.gif) 时,
时,--数学文科.files/image392.gif) ,
,
此时--数学文科.files/image394.gif) ∴ 不满足题意,舍去.
∴ 不满足题意,舍去.
--数学文科.files/image396.gif) 当
当--数学文科.files/image398.gif) 时,
时,--数学文科.files/image400.gif) ,
,
此时--数学文科.files/image402.gif) ,
,
∴ --数学文科.files/image404.gif) .
.
--数学文科.files/image406.gif) 当
当--数学文科.files/image408.gif) 时,
时,--数学文科.files/image410.gif) .
.
此时--数学文科.files/image412.gif) ,
不满足题意,舍去.
,
不满足题意,舍去.
综上所述,所求通项为--数学文科.files/image404.gif) .
.
| 13 |
| 4 |
| 5 |
| 2 |
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,-265<a10<-125,求数列{an}的通项公式. 查看习题详情和答案>>
在直角坐标平面上有一点列P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对一切正整数n,点Pn在函数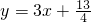 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求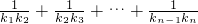 ;
;
(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,-265<a10<-125,求数列{an}的通项公式.
查看习题详情和答案>>
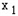 ,y1),P2(x2,y2),…,Pn(xn,yn),…,对一切正整数n,点Pn在函数
,y1),P2(x2,y2),…,Pn(xn,yn),…,对一切正整数n,点Pn在函数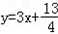 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以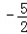 为首项,﹣1为公差的等差数列{xn}.
为首项,﹣1为公差的等差数列{xn}.(1)求点Pn的坐标;
(2)设抛物线列
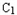 ,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求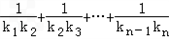 ;
;(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{
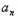 }的任一项
}的任一项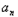 ∈S∩T,其中a1是S∩T中的最大数,﹣265<a10<﹣125,求数列{
∈S∩T,其中a1是S∩T中的最大数,﹣265<a10<﹣125,求数列{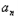 }的通项公式.
}的通项公式.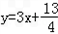 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以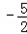 为首项,﹣1为公差的等差数列{xn}.
为首项,﹣1为公差的等差数列{xn}.(1)求点Pn的坐标;
(2)设抛物线列
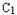 ,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求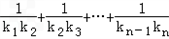 ;
;(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,﹣265<a10<﹣125,求数列{an}的通项公式.
| 13 |
| 4 |
| 5 |
| 2 |
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| kn-1kn |
(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,-265<a10<-125,求数列{an}的通项公式.