已知中心在原点O，焦点F₁、F₂在x轴上的椭圆E经过点C（2，2），且抛物线的焦点为F₁.

（Ⅰ）求椭圆E的方程；

（Ⅱ）垂直于OC的直线l与椭圆E交于A、B两点，当以AB为直径的圆P与y轴相切时，求直线l的方程和圆P的方程.

【解析】本试题主要考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。第一问中，设出椭圆的方程，然后结合抛物线的焦点坐标得到，又因为，这样可知得到。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到

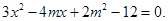，再利用可以结合韦达定理求解得到m的值和圆p的方程。

解：(Ⅰ)设椭圆E的方程为

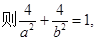①………………………………1分

  ②………………２分

  ③       由①、②、③得a²=12,b²=6…………3分

所以椭圆E的方程为…………………………4分

(Ⅱ)依题意，直线OC斜率为1，由此设直线l的方程为y=-x+m，……………5分

 代入椭圆E方程，得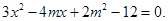…………………………6分

………………………7分

、………………8分

………………………9分

……………………………10分

    当m=3时，直线l方程为y=-x+3，此时，x₁ +x₂=4，圆心为（2，1），半径为2，

圆P的方程为（x-2）²+(y-1)²=4；………………………………11分

同理，当m=－3时，直线l方程为y=-x－3，

圆P的方程为（x+2）²+(y+1)²=4

已知曲线上动点到定点与定直线的距离之比为常数．

（1）求曲线的轨迹方程；

（2）若过点引曲线C的弦AB恰好被点平分，求弦AB所在的直线方程；

（3）以曲线的左顶点为圆心作圆：，设圆与曲线交于点与点，求的最小值，并求此时圆的方程.

【解析】第一问利用（1）过点作直线的垂线，垂足为D.

代入坐标得到

第二问当斜率k不存在时，检验得不符合要求；

当直线l的斜率为k时，；，化简得

第三问点N与点M关于X轴对称，设，， 不妨设．

由于点M在椭圆C上，所以．

由已知，则

，

由于，故当时，取得最小值为．

计算得，，故，又点在圆上，代入圆的方程得到．  

故圆T的方程为：

已知函数的图象过坐标原点O,且在点处的切线的斜率是.

（Ⅰ）求实数的值； 

（Ⅱ）求在区间上的最大值；

（Ⅲ）对任意给定的正实数，曲线上是否存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上？说明理由.

【解析】第一问当时，，则。

依题意得：，即    解得

第二问当时，，令得，结合导数和函数之间的关系得到单调性的判定，得到极值和最值

第三问假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

（Ⅰ）当时，，则。

依题意得：，即    解得

（Ⅱ）由（Ⅰ）知，

①当时，，令得

当变化时，的变化情况如下表：

又，，。∴在上的最大值为2.

②当时, .当时, ,最大值为0；

当时, 在上单调递增。∴在最大值为。

综上，当时，即时，在区间上的最大值为2；

当时，即时，在区间上的最大值为。

（Ⅲ）假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

若，则代入（*）式得：

即，而此方程无解，因此。此时，

代入（*）式得：    即   （**）

令 ，则

∴在上单调递增，  ∵     ∴,∴的取值范围是。

∴对于，方程（**）总有解，即方程（*）总有解。

因此，对任意给定的正实数，曲线上存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上

已知点为圆上的动点，且不在轴上，轴，垂足为，线段中点的轨迹为曲线，过定点任作一条与轴不垂直的直线，它与曲线交于、两点。

（I）求曲线的方程；

（II）试证明：在轴上存在定点，使得总能被轴平分

【解析】第一问中设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为

第二问中，设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　

∵，∴

确定结论直线与曲线总有两个公共点．

然后设点,的坐标分别, ，则，  

要使被轴平分，只要得到。

（1）设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为．  ………………2分       

（2）设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　，……5分            

∵，∴，

∴直线与曲线总有两个公共点．（也可根据点M在椭圆的内部得到此结论）

………………6分

设点,的坐标分别, ，则，   

要使被轴平分，只要，            ………………9分

即，，        ………………10分

也就是，，

即，即只要　 ………………12分　 

当时，（＊）对任意的s都成立，从而总能被轴平分．

所以在x轴上存在定点，使得总能被轴平分