摘要： 解:(1)记“甲击中目标的次数减去乙击中目标的次数为2 为事件A.则
网址：http://m.1010jiajiao.com/timu_id_507618[举报]
甲、乙两人各进行3次射击,甲每次击中目标的概率为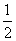
,乙每次击中目标的概率为
.
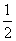,乙每次击中目标的概率为.(1)记甲击中目标的次数为ξ,求ξ的概率分布及数学期望Eξ;
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.
查看习题详情和答案>>
甲、乙两个射手进行射击训练，甲击中目标的概率为
，乙击中目标的概率为
，每人各射击两发子弹为一个“单位射击组”，若甲击中目标的次数比乙击中目标的次数多，则称此组为“单位进步组”．
（1）求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数ξ，求ξ的分布列与数学期望． 查看习题详情和答案>>
| 2 |
| 3 |
| 3 |
| 4 |
（1）求一个“单位射击组”为“单位进步组”的概率；
（2）记完成三个“单位射击组”后出现“单位进步组”的次数ξ，求ξ的分布列与数学期望． 查看习题详情和答案>>
（2012•红桥区一模）甲、乙两人各进行3次射击，甲每次击中目标的概率为
，乙每次击中目标的概率
，假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响．
（Ⅰ）求甲至少有1次未击中目标的概率；
（Ⅱ）记甲击中目标的次数为ξ，求ξ的概率分布及数学期望Eξ；
（Ⅲ）求甲恰好比乙多击中目标2次的概率．
查看习题详情和答案>>
| 3 |
| 4 |
| 2 |
| 3 |
（Ⅰ）求甲至少有1次未击中目标的概率；
（Ⅱ）记甲击中目标的次数为ξ，求ξ的概率分布及数学期望Eξ；
（Ⅲ）求甲恰好比乙多击中目标2次的概率．
，乙每次击中目标的概率为
.
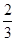，求