摘要：由＞0.得＜x＜k.由＜0.得0＜x＜.∴函数g 上单调递减,在(, k)上单调递增. -7分故函数g(x)的最小值是:ymin=g()=kln. -8分
网址：http://m.1010jiajiao.com/timu_id_504755[举报]
已知函数f(x)=kx+m，当x∈[a1，b1]时，f(x)的值域为[a2，b2]，当x∈[a2，b2]时，f(x)的值域为[a3，b3]，依次类推，一般地，当x∈[an-1，bn-1]时，f(x)的值域为[an，bn]，其中k，m为常数，且a1=0，b1=1，
(Ⅰ)若k=1，求数列{an}，{bn}的通项公式；
(Ⅱ)若m=2，问是否存在常数k＞0，使得数列{bn}满足
？若存在，求k的值；若不存在，请说明理由；
( Ⅲ)若k＜0，设数列{an}，{bn}的前n项和分别为Sn，Tn，求(T1+T2+…+ T2010)-(S1+S2+…+S2010)。
查看习题详情和答案>>
(Ⅰ)若k=1，求数列{an}，{bn}的通项公式；
(Ⅱ)若m=2，问是否存在常数k＞0，使得数列{bn}满足
？若存在，求k的值；若不存在，请说明理由；( Ⅲ)若k＜0，设数列{an}，{bn}的前n项和分别为Sn，Tn，求(T1+T2+…+ T2010)-(S1+S2+…+S2010)。
已知函数f(x)=mx3-
x的图象上，以N（1，n）为切点的切线的倾斜角为
，
（1）求m，n的值；
（2）是否存在最小的正整数k，使得不等式f（x）≤k-1999对于x∈[-1，3]恒成立？如果存在，请求出最小的正整数k；如果不存在，请说明理由；
（3）求证：|f(sinx)+f(cosx)|＜f(t+
)(x∈R，t＞0)．
查看习题详情和答案>>
| 1 |
| 3 |
| π |
| 4 |
（1）求m，n的值；
（2）是否存在最小的正整数k，使得不等式f（x）≤k-1999对于x∈[-1，3]恒成立？如果存在，请求出最小的正整数k；如果不存在，请说明理由；
（3）求证：|f(sinx)+f(cosx)|＜f(t+
| 1 |
| 2t |
设函数f（x）=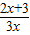
（x＞0），数列{an}满足
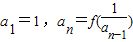（n∈N*，且n≥2）．
（1）求数列{an}的通项公式；
（2）设Tn=a1a2-a2a3+a3a4-a4a5+…+（-1）n-1anan+1，若Tn≥tn2对n∈N*恒成立，求实数t的取值范围；
（3）是否存在以a1为首项，公比为q（0＜q＜5，q∈N*）的数列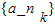
，k∈N*，使得数列
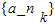中每一项都是数列{an}中不同的项，若存在，求出所有满足条件的数列{nk}的通项公式；若不存在，说明理由．
查看习题详情和答案>>
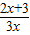（x＞0），数列{an}满足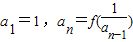（n∈N*，且n≥2）．（1）求数列{an}的通项公式；
（2）设Tn=a1a2-a2a3+a3a4-a4a5+…+（-1）n-1anan+1，若Tn≥tn2对n∈N*恒成立，求实数t的取值范围；
（3）是否存在以a1为首项，公比为q（0＜q＜5，q∈N*）的数列
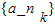，k∈N*，使得数列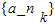中每一项都是数列{an}中不同的项，若存在，求出所有满足条件的数列{nk}的通项公式；若不存在，说明理由．查看习题详情和答案>>
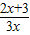（x＞0），数列{an}满足
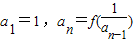（n∈N*，且n≥2）．
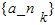，k∈N*，使得数列
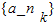中每一项都是数列{an}中不同的项，若存在，求出所有满足条件的数列{nk}的通项公式；若不存在，说明理由．
（x＞0），数列{an}满足
（n∈N*，且n≥2）．
，k∈N*，使得数列
中每一项都是数列{an}中不同的项，若存在，求出所有满足条件的数列{nk}的通项公式；若不存在，说明理由．