20．(1)解:由椭圆方程及双曲线方程可得点B(0.2).直线l的方程是． .且AC在直线l上运动. 可设.则AC的垂直平分线方程为 ① AB的垂直平分线方程为 ②——青夏教育精英家教网——

摘要：20．(1)解:由椭圆方程及双曲线方程可得点B(0.2).直线l的方程是． .且AC在直线l上运动. 可设.则AC的垂直平分线方程为 ① AB的垂直平分线方程为 ②

网址：http://m.1010jiajiao.com/timu_id_501741[举报]

已知椭圆C₁的方程为

+y²=1，双曲线C₂的左、右焦点分别为C₁的左、右顶点，而C₂的左、右顶点分别是C₁的左、右焦点．
（Ⅰ）求双曲线C₂的方程；
（Ⅱ）若直线l：y=kx+

与椭圆C₁及双曲线C₂都恒有两个不同的交点，且l与C₂的两个交点A和B满足

＜6（其中O为原点），求k的取值范围．查看习题详情和答案>>

（2013•浦东新区二模）（1）设椭圆C₁：

=1与双曲线C₂：9x2-

=1有相同的焦点F₁、F₂，M是椭圆C₁与双曲线C₂的公共点，且△MF₁F₂的周长为6，求椭圆C₁的方程；
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．
（2）如图，已知“盾圆D”的方程为y2=

-12(x-4) (3＜x≤4)

．设“盾圆D”上的任意一点M到F（1，0）的距离为d₁，M到直线l：x=3的距离为d₂，求证：d₁+d₂为定值；
（3）由抛物线弧E₁：y²=4x（0≤x≤

）与第（1）小题椭圆弧E₂：

≤x≤a）所合成的封闭曲线为“盾圆E”．设过点F（1，0）的直线与“盾圆E”交于A、B两点，|FA|=r₁，|FB|=r₂且∠AFx=α（0≤α≤π），试用cosα表示r₁；并求

的取值范围．

查看习题详情和答案>>

已知椭圆C₁的方程为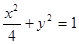，双曲线C₂的左、右焦点分别为C₁的左、右顶点，而C₂的左、右顶点分别是C₁的左、右焦点。

(1) 求双曲线C₂的方程；

(2) 若直线l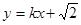：与椭圆C₁及双曲线C₂恒有两个不同的交点，且l与C₂的两个交点A和B满足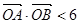(其中O为原点)，求k的取值范围。

查看习题详情和答案>>

（本小题满分12分）

已知椭圆C₁的方程为，双曲线C₂的左、右焦点分别为C₁的左、右顶点，而C₂的左、右顶点分别是C₁的左、右焦点．

（1）求双曲线C₂的方程；

（2）若直线与椭圆C₁及双曲线C₂都恒有两个不同的交点，且l与C₂的两个交点A和B满足（其中O为原点），求k的取值范围．

查看习题详情和答案>>

已知椭圆C₁的方程为

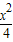+y²=1，双曲线C₂的左、右焦点分别为C₁的左、右顶点，而C₂的左、右顶点分别是C₁的左、右焦点．
（Ⅰ）求双曲线C₂的方程；
（Ⅱ）若直线l：y=kx+

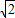与椭圆C₁及双曲线C₂都恒有两个不同的交点，且l与C₂的两个交点A和B满足

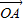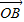＜6（其中O为原点），求k的取值范围．
查看习题详情和答案>>