摘要:即存在正整数m=8.使得对于任意正整数n都有
网址:http://m.1010jiajiao.com/timu_id_4966[举报]
(2011•重庆二模)已知数列{an}的前n项和为Sn,
=(Sn,1),
=(-1,2an+2n),
⊥
.
(Ⅰ)证明数列{
}为等差数列,并求数列{an}的通项公式;
(Ⅱ)设bn=
,是否存在正整数n0,使得对于任意的k∈N*,都有不等式bk≤bn成立?若存在,求出n0的值;若不存在,请说明理由;
(Ⅲ)设Tn=|S1|-|S2|+…+|Sn|,求证:
>
an.
查看习题详情和答案>>
| a |
| b |
| a |
| b |
(Ⅰ)证明数列{
| an |
| 2n-1 |
(Ⅱ)设bn=
| (n-2011)an |
| n+1 |
(Ⅲ)设Tn=|S1|-|S2|+…+|Sn|,求证:
| T0+Sn |
| 2 |
| 2-n |
| 1+n |
在数列 中,如果存在非零的常数
中,如果存在非零的常数 ,使得
,使得 对于任意正整数
对于任意正整数 均成立,那么就称数列
均成立,那么就称数列 为周期数列,其中
为周期数列,其中 叫做数列
叫做数列 的周期. 已知数列
的周期. 已知数列 满足
满足 ,若
,若 ,当数列
,当数列 的周期为
的周期为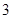 时,则数列
时,则数列 的前
的前 项的和
项的和 为(
)
为(
)
A. B.
B. C.
C. D.
D.
查看习题详情和答案>>
已知数列{an}的前n项和为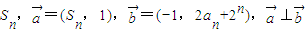 .
.
(Ⅰ)证明数列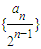 为等差数列,并求数列{an}的通项公式;
为等差数列,并求数列{an}的通项公式;
(Ⅱ)设 ,是否存在正整数n,使得对于任意的k∈N*,都有不等式bk≤bn成立?若存在,求出n的值;若不存在,请说明理由;
,是否存在正整数n,使得对于任意的k∈N*,都有不等式bk≤bn成立?若存在,求出n的值;若不存在,请说明理由;
(Ⅲ)设Tn=|S1|-|S2|+…+|Sn|,求证: .
.
查看习题详情和答案>>
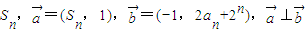 .
.(Ⅰ)证明数列
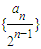 为等差数列,并求数列{an}的通项公式;
为等差数列,并求数列{an}的通项公式;(Ⅱ)设
 ,是否存在正整数n,使得对于任意的k∈N*,都有不等式bk≤bn成立?若存在,求出n的值;若不存在,请说明理由;
,是否存在正整数n,使得对于任意的k∈N*,都有不等式bk≤bn成立?若存在,求出n的值;若不存在,请说明理由;(Ⅲ)设Tn=|S1|-|S2|+…+|Sn|,求证:
 .
.查看习题详情和答案>>
在数列 中,如果存在非零的常数
中,如果存在非零的常数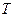 ,使得
,使得 对于任意正整数
对于任意正整数 均成立,那么就称数列
均成立,那么就称数列 为周期数列,其中
为周期数列,其中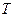 叫做数列
叫做数列 的周期. 已知数列
的周期. 已知数列 满足
满足 ,若
,若 ,当数列
,当数列 的周期为
的周期为 时,则数列
时,则数列 的前
的前 项的和
项的和 为( )
为( )
A.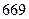 | B. | C. | D. |
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|