摘要：因为为的角平分线.所以.即
网址：http://m.1010jiajiao.com/timu_id_495804[举报]
如图，在△ABC中，AB=2，AC=BC=
．
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=-1．
当x2=3，即y2=3，∴y3=
，y4=-．
所以，原方程的解是y1=1，y2=-1，y3=，y4=-．
再如x2-2=4
，可设y=，用同样的方法也可求解．
查看习题详情和答案>>
如图，在△ABC中，AB=2，AC=BC=
．
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=-1．
当x2=3，即y2=3，∴y3=
，y4=-
．
所以，原方程的解是y1=1，y2=-1，y3=
，y4=-
．
再如x2-2=4
，可设y=
，用同样的方法也可求解．
查看习题详情和答案>>
．（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=-1．
当x2=3，即y2=3，∴y3=
，y4=-．所以，原方程的解是y1=1，y2=-1，y3=
，y4=-．再如x2-2=4
，可设y=，用同样的方法也可求解．
查看习题详情和答案>>
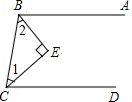有这样一道题：如图所示，已知BA∥CD，BE平分∠ABC，CE平分∠BCD，试判断∠1与∠2的度数有怎样的关系，并说明理由．小丽的判断是∠1与∠2互余，这是正确的，但是她写的说明不完整，请你给予补充．
因为BE是∠ABC的平分线，所以∠2=
| 1 |
| 2 |
∠ABC
∠ABC
．又因为CE是∠BCD的平分线，所以∠1=| 1 |
| 2 |
∠BCD
∠BCD
，于是∠1+∠2=| 1 |
| 2 |
∠ABC
∠ABC
+∠BCD
∠BCD
）．而AB∥CD，根据两直线平行，同旁内角互补，得
∠ABC
∠ABC
+∠BCD
∠BCD
=180°
180°
，所以∠1+∠2=90°，即∠1与∠2互余．有这样一道题：
如图所示，已知BA∥CD，BE平分∠ABC，CE平分∠BCD，试判断∠1与∠2的度数有怎样的关系，并说明理由．小丽的判断是∠1与∠2互余，这是正确的，但是她写的说明不完整，请你给予补充．
因为BE是∠ABC的平分线，所以∠2=
______．又因为CE是∠BCD的平分线，所以∠1=
______，于是∠1+∠2=
（______+______）．
而AB∥CD，根据两直线平行，同旁内角互补，得______+______=______，所以∠1+∠2=90°，即∠1与∠2互余．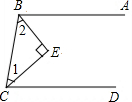
查看习题详情和答案>>
如图所示，已知BA∥CD，BE平分∠ABC，CE平分∠BCD，试判断∠1与∠2的度数有怎样的关系，并说明理由．小丽的判断是∠1与∠2互余，这是正确的，但是她写的说明不完整，请你给予补充．
因为BE是∠ABC的平分线，所以∠2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而AB∥CD，根据两直线平行，同旁内角互补，得______+______=______，所以∠1+∠2=90°，即∠1与∠2互余．
（1）自主阅读：如图1，AD∥BC，连接AB、AC、BD、CD，则S△ABC=S△BCD．
证明：分别过点A和D，作AF⊥BC，DE⊥BC
由AD∥BC，可得AF=DE．
又因为S△ABC=
×BC×AF，S△BCD=
BC×DE
所以S△ABC=S△BCD
由此我们可以得到以下的结论：像图1这样，______．
（2）结论证明：如果一条直线（线段）把一个平面图形的面积分成相等的两部分，我们把这条直线（线段）称为这个平面图形的一条面积等分线（段），如，平行四变形的一条对角线就是平形四边形的一条面积等分线段．
①如图2，梯形ABCD中AB∥DC，连接AC，过点B作BE∥AC，交DC延长线于点E，连接点A和DE的中点P，则AP即为梯形ABCD的面积等分线段，请你写出这个结论成立的理由：
②如图3，四边形ABCD中，AB与CD不平行，S△ADC＞S△ABC，过点A能否做出四边形ABCD的面积等分线（段）？若能，请画出面积等分线（用钢笔或圆珠笔画图，不用写作法），不要证明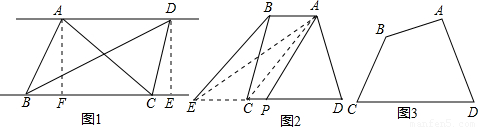
查看习题详情和答案>>
证明：分别过点A和D，作AF⊥BC，DE⊥BC
由AD∥BC，可得AF=DE．
又因为S△ABC=
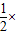×BC×AF，S△BCD=BC×DE所以S△ABC=S△BCD
由此我们可以得到以下的结论：像图1这样，______．
（2）结论证明：如果一条直线（线段）把一个平面图形的面积分成相等的两部分，我们把这条直线（线段）称为这个平面图形的一条面积等分线（段），如，平行四变形的一条对角线就是平形四边形的一条面积等分线段．
①如图2，梯形ABCD中AB∥DC，连接AC，过点B作BE∥AC，交DC延长线于点E，连接点A和DE的中点P，则AP即为梯形ABCD的面积等分线段，请你写出这个结论成立的理由：
②如图3，四边形ABCD中，AB与CD不平行，S△ADC＞S△ABC，过点A能否做出四边形ABCD的面积等分线（段）？若能，请画出面积等分线（用钢笔或圆珠笔画图，不用写作法），不要证明
查看习题详情和答案>>