摘要：如图所示..同一平面内角的平分线正好与成的角均为．过此时的角平分线作平面.使其垂直于所在的平面.当绕着点在平面内按逆时针方向转动时.与所成的角由增大到90º.再由90º减小到.符合条件的直线有2条．
网址：http://m.1010jiajiao.com/timu_id_491547[举报]
(经典回放)如图所示，若从点O所作的两条射线OM、ON上分别有点M1、M2与点N1、N2，则三角形面积之比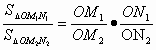
．若从点O所作的不在同一平面内的三条射线OP、OQ和OR上，分别有点P1、P2，点Q1、Q2和点R1、R2，则类似的结论为_________．
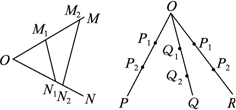
如图，AB是底部B不可到达的一个塔型建筑物，A为塔的最高点．现需在塔对岸测出塔高AB，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底B在同一水平面内的一条基线CD，使C，D，B不在同一条直线上，测出∠DCB及∠CDB的大小(分别用α，β表示测得的数据)以及C，D间的距离(用s表示测得的数据)，另外需在点C测得塔顶A的仰角(用
表示测量的数据)，就可以求得塔高AB．乙同学的方法是：选一条水平基线EF，使E，F，B三点在同一条直线上．在E，F处分别测得塔顶A的仰角(分别用α，β表示测得的数据)以及E，F间的距离(用s表示测得的数据)，就可以求得塔高AB．
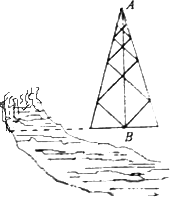
请从甲或乙的想法中选出一种测量方法，写出你的选择并按如下要求完成测量计算：①画出测量示意图；②用所叙述的相应字母表示测量数据，画图时C，D，B按顺时针方向标注，E，F按从左到右的方向标注；③求塔高AB．
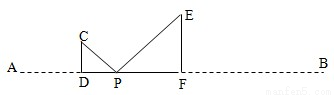
已知：点P为线段AB上的动点（与A，B两点不重合）．在同一平面内，把线段AP，BP分别折成△CDP，△EFP，其中∠CDP=∠EFP=90°，且D，P，F三点共线，如图所示．（1）若△CDP，△EFP均为等腰三角形，且DF=2，求AB的长．
（2）若AB=12，tan∠C=
| 4 | 3 |
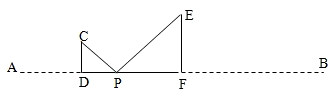已知：点P为线段AB上的动点（与A，B两点不重合）．在同一平面内，把线段AP，BP分别折成△CDP，△EFP，其中∠CDP=∠EFP=90°，且D，P，F三点共线，如图所示．
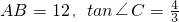，且以C，D，P为顶点的三角形和以E，F，P为顶点的三角形相似，求四边形CDFE的面积的最小值．
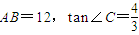，且以C，D，P为顶点的三角形和以E，F，P为顶点的三角形相似，求四边形CDFE的面积的最小值．