摘要:注:①是增量.我们也称为“改变量 .因为可正.可负.但不为零.
网址:http://m.1010jiajiao.com/timu_id_491123[举报]
将十天干、十二地支按顺序依次排列,若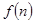 表示处于第
表示处于第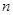 个位置的天干或地
个位置的天干或地
支,.
|
|
十天干 |
十二地支 |
||||||||||||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
|
甲 |
乙 |
丙 |
丁 |
戊 |
己 |
庚 |
辛 |
壬 |
癸 |
子 |
丑 |
寅 |
卯 |
辰 |
巳 |
午 |
未 |
申 |
酉 |
戌 |
亥 |
如上表,即: ,
, .定义函数
.定义函数 .
.
(1) 分别求 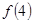 ,
,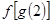 ,
,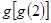
(2) 2010年是庚寅年,我们也可以用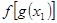
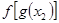 的表示形式来表示该年,求
的表示形式来表示该年,求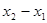
的值
查看习题详情和答案>>
将质地均匀的两枚硬币抛掷一次,若两枚硬币的正面朝上,我们称之为一次“成功抛掷”.
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
查看习题详情和答案>>
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
将质地均匀的两枚硬币抛掷一次,若两枚硬币的正面朝上,我们称之为一次“成功抛掷”.
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
查看习题详情和答案>>
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
将质地均匀的两枚硬币抛掷一次,若两枚硬币的正面朝上,我们称之为一次“成功抛掷”.
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
查看习题详情和答案>>
(1)求三次这样的抛掷,至少两次是“成功抛掷”的概率;
(2)三次这样的抛掷后,再抛掷一枚硬币,若正面朝上,也称为一次“成功抛掷”,记四次抛掷后“成功抛掷”的次数为ε,求ε的分布列和期望.
 (2013•房山区一模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.
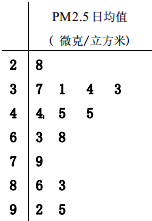
(2013•房山区一模)PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2012年全年每天的PM2.5监测数据中随机的抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(Ⅰ)从这15天的PM2.5日均监测数据中,随机抽出三天数据,求恰有一天空气质量达到一级的概率;
(Ⅱ)从这15天的数据中任取三天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列和数学期望;
(Ⅲ)根据这15天的PM2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级.