摘要：①函数f(x)在点处有定义,②存在,③函数f(x)在点处的极限值等于该点的函数值.即.

网址：http://m.1010jiajiao.com/timu_id_491105[举报]

已知函数f（x）=mx-lnx-3（m∈R）．
（1）讨论函数f（x）在定义域内的极值点的个数；
（2）若函数f（x）在x=1处取得极值，存在x∈（0，+∞）使f（x）≤nx-4有解，求实数n的取值范围；
（3）当0＜a＜b＜4且b≠e时试比较

查看习题详情和答案>>

已知函数f（x）=mx²-x+lnx．
（1）当m=-1时，求f（x）的最大值；
（2）若在函数f（x）的定义域内存在区间D，使得该函数在区间D上为减函数，求m的取值范围；
（3）当m＞0时，若曲线C：y=f（x）在点x=1处的切线l与C有且只有一个公共点，求m的值．

查看习题详情和答案>>

已知函数f（x）=px³+qx²+2在x=2处取得极小值-2．
（1）设T（x）=f（x）+m，若T（x）有三个零点，求实数m的范围；
（2）是否存在实数k，当a+b≤2时，使得函数g(x)=

f′(x)+k在定义域[a，b]上值域为[a，b]（a≠b），若存在，求k的范围；若不存在，说明理由．

查看习题详情和答案>>

已知函数f（x）=lnx，g（x）= $数学公式$ x²-bx（b为常数）．
（1）函数f（x）的图象在点（1，f（1））处的切线与g（x）的图象相切，求实数b的值；
（2）设h（x）=f（x）+g（x），若函数h（x）在定义域上存在单调减区间，求实数b 的取值范围；
（3）若b＞1，对于区间[1，2]上的任意两个不相等的实数x₁，x₂，都有|f（x₁）-f（x₂）|＞|g（x₁）-g（x₂）|成立，求b的取值范围．

查看习题详情和答案>>

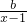已知函数f（x）=ax+ $数学公式$ -a（a∈R，a≠0）在x=3处的切线方程为（2a-1）x-2y+3=0
（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值；
（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m-x）=k对于定义域内的任意x都成立；
（3）若方程f（x）=t（x²-2x+3）|x|有三个解，求实数t的取值范围．

查看习题详情和答案>>