摘要：⑶等轴双曲线:双曲线称为等轴双曲线.其渐近线方程为.离心率.
网址：http://m.1010jiajiao.com/timu_id_490723[举报]
双曲线
＝1(a＞0，b＞0)的几何性质
(1)范围：________，这说明该双曲线在不等式________与________所表示的区域内．
(2)对称性：关于________对称．双曲线的对称中心叫做双曲线的________．
(3)顶点：顶点的坐标分别为________、________，实轴的长是________，虚轴的长是________．
(4)渐近线：其渐近线方程是________．实轴和虚轴等长的双曲线叫做________．
(5)离心率：双曲线的焦距与实轴长的比e＝
，叫做双曲线的________．其中e∈________．当e越大时，双曲线的开口也越________．
双曲线
＝1(a＞0，b＞0)的几何性质
(1)范围：________，这说明该双曲线在不等式________与________所表示的区域内．
(2)对称性：关于________对称．双曲线的对称中心叫做双曲线的________．
(3)顶点：顶点的坐标分别为________、________，实轴的长是________，虚轴长是________．
(4)渐近线：其渐近线方程是________．实轴和虚轴等长的双曲线叫做________．
(5)离心率：双曲线的焦距与实轴长的比e＝
，叫做双曲线的________．其中e∈________．当e越大时，双曲线的开口也越________．
已知双曲线C：
-
=1(a＞0，b＞0)的左、右焦点分别为F1，F2，离心率为e．直线l：y=ex+a与x轴、y轴分别交于A，B两点．
（1）求证：直线l与双曲线C只有一个公共点；
（2）设直线l与双曲线C的公共点为M，且
=λ
，证明：λ+e2=1；
（3）设P是点F1关于直线l的对称点，当△PF1F2为等腰三角形时，求e的值． 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
（1）求证：直线l与双曲线C只有一个公共点；
（2）设直线l与双曲线C的公共点为M，且
| AM |
| AB |
（3）设P是点F1关于直线l的对称点，当△PF1F2为等腰三角形时，求e的值． 查看习题详情和答案>>
的左、右焦点分别为F1，F2，离心率为e．直线l：y=ex+a与x轴、y轴分别交于A，B两点．
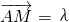
，证明：λ+e2=1；
的左、右焦点分别为F1，F2，离心率为e．直线l：y=ex+a与x轴、y轴分别交于A，B两点．
，证明：λ+e2=1；