网址:http://m.1010jiajiao.com/timu_id_487435[举报]
曲线运动万有引力.files/image232.jpg)
曲线运动万有引力.files/image234.jpg) 一、选择题
一、选择题
1、根据图象分析:若沿x轴作匀速运动,通过图1分析可知,y方向先减速后加速;若沿y轴方向作匀速运动,通过图2分析可知,x方向先加速后减速。
答案:B
2、乙船能到达A点,则vcos600=u,
曲线运动万有引力.files/image235.jpg) 过河时间t满足:t = H/( vsin600), 甲、乙两船沿垂直于河岸方向的分速度相同,故过河时间相同。在t时间内甲船沿河岸方向的位移为s= (vcos600 + u )t=
过河时间t满足:t = H/( vsin600), 甲、乙两船沿垂直于河岸方向的分速度相同,故过河时间相同。在t时间内甲船沿河岸方向的位移为s= (vcos600 + u )t=曲线运动万有引力.files/image191.gif) 。
。
答案:D
3、根据万有引力定律:曲线运动万有引力.files/image237.gif) ,得:T=
,得:T=曲线运动万有引力.files/image197.gif)
答案:A
4、质点在A、B、C、D四点离开轨道,分别做下抛、平抛、上抛、平抛运动。很明显,在A点离开轨道比在C、D两点离开轨道在空间时间短。通过计算在A点下抛落地时间为tA=(6曲线运动万有引力.files/image240.gif) -4)s,在B点平抛落地时间tB=4
-4)s,在B点平抛落地时间tB=4曲线运动万有引力.files/image242.gif) s,显然,在A点离开轨道后在空中时间最短。根据机械能守恒,在D刚抛出时机械能最大,所以落地时速度最大。
s,显然,在A点离开轨道后在空中时间最短。根据机械能守恒,在D刚抛出时机械能最大,所以落地时速度最大。
答案:AD
曲线运动万有引力.files/image207.jpg) 5、在轨道上向其运行方向弹射一个物体,由于质量远小于空间站的质量,空间站仍沿原方向运动。根据动量守恒,弹出后一瞬间,空间站沿原运行方向的速度变小,提供的向心力(万有引力)大于需要的向心力,轨道半径减小,高度降低,在较低的轨道上运行速率变大,周期变小。
5、在轨道上向其运行方向弹射一个物体,由于质量远小于空间站的质量,空间站仍沿原方向运动。根据动量守恒,弹出后一瞬间,空间站沿原运行方向的速度变小,提供的向心力(万有引力)大于需要的向心力,轨道半径减小,高度降低,在较低的轨道上运行速率变大,周期变小。
答案:C
6、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变;但圆周运动的半径减小,需要的向心力变大,向心加速度变大,绳子上的拉力变大。
答案:BD
7、根据万有引力定律:曲线运动万有引力.files/image237.gif) 可得:M=
可得:M=曲线运动万有引力.files/image244.gif) ,可求出恒星质量与太阳质量之比,根据
,可求出恒星质量与太阳质量之比,根据曲线运动万有引力.files/image246.gif) 可得:v=
可得:v=曲线运动万有引力.files/image248.gif) ,可求出行星运行速度与地球公转速度之比。
,可求出行星运行速度与地球公转速度之比。
答案:AD
8、卫星仍围绕地球运行,所以发射速度小
答案:CD
9、同步卫星随地球自转的方向是从东向西,把同步卫星从赤道上空3.6万千米、东经103°处,调整到104°处,相对于地球沿前进方向移动位置,需要增大相对速度,所以应先下降高度增大速度到某一位置再上升到原来的高度。
答案:A
10、开始转动时向心力由静摩擦力提供,但根据F=mrω2可知,B需要的向心力是A的两倍。所以随着转速增大,B的摩擦力首先达到最大静摩擦力。继续增大转速,绳子的张力增大,B的向心力由最大静摩擦力提供,A的向心力由静摩擦力和绳子的张力的合力提供,随着转速的增大,B需要的向心力的增量(绳子张力的增量)比A需要的向心力的增量大,因而A指向圆心的摩擦力逐渐减小直到为0然后反向增大到最大静摩擦力。所以,B受到的静摩擦力先增大,后保持不变;A受到的静摩擦力是先减小后增大;A受到的合外力就是向心力一直在增大。
答案:BD
二、填空题
11、圆盘转动时,角速度的表达式为ω= 曲线运动万有引力.files/image250.gif) , T为电磁打点计的时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应米尺上的刻度值,n为选定的两点间的打点数(含两点)。地纸带上选取两点(间隔尽可能大些)代入上式可求得ω=
6.8rad/s。
, T为电磁打点计的时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应米尺上的刻度值,n为选定的两点间的打点数(含两点)。地纸带上选取两点(间隔尽可能大些)代入上式可求得ω=
6.8rad/s。
12、 (1)斜槽末端切线方向保持水平;从同一高度。
(2)设时间间隔为t, x
= v0t, y2-y1=gt2
,解得: v0=曲线运动万有引力.files/image252.gif) .将x=
.将x=
三、计算题
13.解:⑴在行星表面,质量为m的物体的重力近似等于其受到的万有引力,则
曲线运动万有引力.files/image083.gif)
g=曲线运动万有引力.files/image177.gif)
得:曲线运动万有引力.files/image256.gif)
⑵行星表面的环绕速度即为第一宇宙速度,做匀速圆周运动的向心力是万有引力提供的,则
曲线运动万有引力.files/image258.gif)
v1=曲线运动万有引力.files/image248.gif)
曲线运动万有引力.files/image260.gif) 得:
得:曲线运动万有引力.files/image262.gif)
14.解析:用r表示飞船圆轨道半径,有r =R +H=6.71×l
由万有引力定律和牛顿定律,得 曲线运动万有引力.files/image264.gif) , 式中M表示地球质量,m表示飞船质量,T表示飞船绕地球运行的周期,G表示万有引力常量.
, 式中M表示地球质量,m表示飞船质量,T表示飞船绕地球运行的周期,G表示万有引力常量.
利用曲线运动万有引力.files/image167.gif) 及上式, 得
及上式, 得 曲线运动万有引力.files/image266.gif) ,代入数值解得T=5.28×103s,
,代入数值解得T=5.28×103s,
出舱活动时间t=25min23s=1523s,
航天员绕行地球角度 曲线运动万有引力.files/image268.gif) =1040
=1040
15.解:(1)这位同学对过程的分析错误,物块先沿着圆柱面加速下滑,然后离开圆柱面做斜下抛运动,离开圆柱面时的速率不等于曲线运动万有引力.files/image270.gif) 。
。
(2)a、设物块离开圆柱面时的速率为曲线运动万有引力.files/image272.gif) ,
,
曲线运动万有引力.files/image273.gif)
曲线运动万有引力.files/image275.gif)
曲线运动万有引力.files/image277.gif)
解得:曲线运动万有引力.files/image279.gif)
(2)b、由:曲线运动万有引力.files/image222.gif) 得:
得:
落地时的速率为曲线运动万有引力.files/image195.gif)
曲线运动万有引力.files/image224.gif)
16.解:对子弹和木块应用动量守恒定律:
曲线运动万有引力.files/image281.gif)
所以
曲线运动万有引力.files/image283.gif)
对子弹、木块由水平轨道到最高点应用机械能守恒定律,
取水平面为零势能面:有
曲线运动万有引力.files/image285.gif)
所以 曲线运动万有引力.files/image287.gif)
由平抛运动规律有:曲线运动万有引力.files/image289.gif)
曲线运动万有引力.files/image291.gif)
解得: 曲线运动万有引力.files/image293.gif)
所以,当R =
最大值Smax =
曲线运动万有引力.files/image294.gif)
17.解:(1)
曲线运动万有引力.files/image296.gif)
(2)设人在B1位置刚好看见卫星出现在A1位置,最后
在B2位置看到卫星从A2位置消失,
OA1=2OB1
有曲线运动万有引力.files/image298.gif) ∠A1OB1=∠A2OB2=π/3
∠A1OB1=∠A2OB2=π/3
从B1到B2时间为t
则有 曲线运动万有引力.files/image300.gif)
18.解: (1)设
A、B的圆轨道半径分别为曲线运动万有引力.files/image302.gif) 、
、曲线运动万有引力.files/image304.gif) ,由题意知,A、B做匀速圆周运动的角速 度相同,设其为
,由题意知,A、B做匀速圆周运动的角速 度相同,设其为曲线运动万有引力.files/image306.gif) 。由牛顿运动定律,有
。由牛顿运动定律,有
曲线运动万有引力.files/image308.gif)
曲线运动万有引力.files/image310.gif)
曲线运动万有引力.files/image312.gif)
设
A、B之间的距离为曲线运动万有引力.files/image314.gif) ,又
,又曲线运动万有引力.files/image316.gif) ,由上述各式得
,由上述各式得
曲线运动万有引力.files/image318.gif) , ①
, ①
由万有引力定律,有
曲线运动万有引力.files/image320.gif)
将①代入得
曲线运动万有引力.files/image322.gif)
令
曲线运动万有引力.files/image324.gif)
比较可得
曲线运动万有引力.files/image326.gif) ②
②
(2)由牛顿第二定律,有
曲线运动万有引力.files/image328.gif) ③
③
又可见星 A的轨道半径
曲线运动万有引力.files/image330.gif) ④
④
由②③④式解得
曲线运动万有引力.files/image332.gif) ⑤
⑤
(3)将曲线运动万有引力.files/image334.gif) 代入⑤式,得
代入⑤式,得
曲线运动万有引力.files/image336.gif)
代入数据得
曲线运动万有引力.files/image338.gif) ⑥
⑥
曲线运动万有引力.files/image340.gif) ,将其代入⑥式得
,将其代入⑥式得
曲线运动万有引力.files/image342.gif) ⑦
⑦
可见,曲线运动万有引力.files/image344.gif) 的值随 n的增大而增大,试令
的值随 n的增大而增大,试令曲线运动万有引力.files/image346.gif) ,得
,得
曲线运动万有引力.files/image348.gif) ⑧
⑧
若使⑦式成立,则 n 必大于 2,即暗星
B 的质量曲线运动万有引力.files/image350.gif) 必大于
必大于曲线运动万有引力.files/image352.gif) ,由此得出结
,由此得出结
论:暗星曲线运动万有引力.files/image354.gif) 有可能是黑洞。
有可能是黑洞。
46.伽利略的自由落体实验和加速度实验均被选为最美的实验。
在加速度实验中,伽利略将光滑直木板槽倾斜固定,让铜球从木槽顶端沿斜面由静止滑下;并用水钟测量铜球每次下滑的时间,研究铜球的运动路程与时间的关系。亚里士多德曾预言铜球的运动速度是均匀不变的,伽利略却证明铜球运动的路程与时间的平方成正比。请将亚里士多德的预言和伽利略的结论分别用公式表示(其中路程用s、速度用v、加速度用a、时间用t表示)。亚里士多德的预言: ;伽利略的结论: 。
伽利略的两个实验之所以成功,主要原因是在自由落体实验中,忽略了空气阻力,抓住了重力这一主要因素。在加速度实验中,伽利略选用光滑直木板槽和铜球进行实验研究铜球运动,是为了减小铜球运动过程中的 ,同时抓住 这一主要因素。
47.阅读下列材料:
①早在1785年,卡文迪许在测定空气组成时,除去空气中的O2、N2等已知气体后,发现最后总是留下一个体积不足总体积1/200的小气泡。
②1892年,瑞利在测定氮气密度时,从空气中得到的氮气密度为1.2572g/L,而从氨分解得到的氮气密度为1.2508g/L。两者相差0.0064g/L。
③瑞利和拉姆赛共同研究后认为:以上两个实验中的“小误差”可能有某种必然的联系,并预测大气中含有某种较重的未知气体。经反复实验,他们终于发现了化学性质极不活泼的惰性气体——氩。
请回答下列问题:
空气缓慢通过下图a~d装置时,依次除去的气体是…………………( )

A.O2、N2、H2O、CO2 B.CO2、H2O、O2、N2
C.H2O、CO2、N2、O2 D.N2、O2、CO2、H2O
材料①②中的“小误差”对测定空气组成和氮气密度的实验而言是 (填“主要因素”或“次要因素”)。
材料③中科学家抓住了“小误差”而获得重大发现说明 。
48.某学生为了证明植物呼吸时放出二气化碳,设计了如下图的实验装置,其中绿色植物生长旺盛。将装置在黑暗中放置24小时后观察结果。试分析:该装置放在黑暗中的作用是 ;该实验除须在黑暗中完成外,还应注意 。
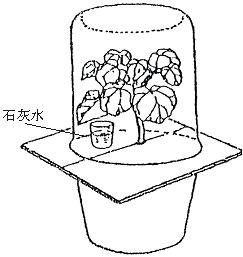
在实验中,有同学提出,需要同时进行另一组其他条件相同但不放植物的实验。你认为有没有意义?简述原因。
查看习题详情和答案>>如图,一位身高1.80m的跳高运动员擅长背越式跳高,他经过25m弧线助跑,下蹲0.2m蹬腿、起跳,划出一道完美的弧线,创造出他的个人最好成绩2.39m(设其重心C上升的最大高度实际低于横杆0.1m).如果他在月球上采用同样的方式起跳和越过横杆,请估算他能够跃过横杆的高度为多少?
某同学认为:该运动员在地球表面能够越过的高度H=
 +0.1,则有v=….
+0.1,则有v=….该名运动员在月球上也以v起跳,能够越过的高度H’=
 +0.1….
+0.1….根据万有引力定律,月球表面的重力加速度为地球表面重力加速度的
 ,所以H′=….
,所以H′=….你觉得这位同学的解答是否合理?如果是,请完成计算;如果你觉得不够全面,请说明理由,并请并用你自己的方法算出相应的结果.
 查看习题详情和答案>>
查看习题详情和答案>>
 辨析题:
辨析题:如图,一位身高1.80m的跳高运动员擅长背越式跳高,他经过25m弧线助跑,下蹲0.2m蹬腿、起跳,划出一道完美的弧线,创造出他的个人最好成绩2.39m(设其重心C上升的最大高度实际低于横杆0.1m).如果他在月球上采用同样的方式起跳和越过横杆,请估算他能够跃过横杆的高度为多少?
某同学认为:该运动员在地球表面能够越过的高度H=
| v02 |
| 2g地 |
该名运动员在月球上也以v0起跳,能够越过的高度H’=
| v02 |
| 2g月 |
根据万有引力定律,月球表面的重力加速度为地球表面重力加速度的
| 1 |
| 6 |
你觉得这位同学的解答是否合理?如果是,请完成计算;如果你觉得不够全面,请说明理由,并请并用你自己的方法算出相应的结果.
(14分)
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
【解析】:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算对)
23.【题文】(16分)
 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经![]() 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
查看习题详情和答案>>