网址:http://m.1010jiajiao.com/timu_id_487396[举报]
一、选择题
1、B 2、C 3、AC 4、D 5、BC 6BC
7、A 解析:由题意知,地面对物块A的摩擦力为0,对物块B的摩擦力为%20牛顿定律在直线运动中的应用.files/image286.gif) 。
。
对A、B整体,设共同运动的加速度为a,由牛顿第二定律有:
%20牛顿定律在直线运动中的应用.files/image288.gif)
对B物体,设A对B的作用力为%20牛顿定律在直线运动中的应用.files/image290.gif) ,同理有
,同理有
%20牛顿定律在直线运动中的应用.files/image292.gif)
联立以上三式得:%20牛顿定律在直线运动中的应用.files/image294.gif)
8、B 9、A 10、B
二、实验题
11、⑴ 不变 ⑵ AD ⑶ABC ⑷某学生的质量
三、计算题
12、解析:由牛顿第二定律得:mg-f=ma
%20牛顿定律在直线运动中的应用.files/image296.gif)
抛物后减速下降有:%20牛顿定律在直线运动中的应用.files/image298.gif)
Δv=a/Δt
解得:%20牛顿定律在直线运动中的应用.files/image300.gif)
13、解析:人相对木板奔跑时,设人的质量为%20牛顿定律在直线运动中的应用.files/image302.gif) ,加速度为
,加速度为%20牛顿定律在直线运动中的应用.files/image304.gif) ,木板的质量为M,加速度大小为
,木板的质量为M,加速度大小为%20牛顿定律在直线运动中的应用.files/image306.gif) ,人与木板间的摩擦力为
,人与木板间的摩擦力为%20牛顿定律在直线运动中的应用.files/image308.gif) ,根据牛顿第二定律,对人有:
,根据牛顿第二定律,对人有:%20牛顿定律在直线运动中的应用.files/image310.gif) ;
;
(2)设人从木板左端开始距到右端的时间为%20牛顿定律在直线运动中的应用.files/image312.gif) ,对木板受力分析可知:
,对木板受力分析可知:%20牛顿定律在直线运动中的应用.files/image314.gif) 故
故%20牛顿定律在直线运动中的应用.files/image316.gif) ,方向向左;
,方向向左;
由几何关系得:%20牛顿定律在直线运动中的应用.files/image318.gif) ,代入数据得:
,代入数据得:%20牛顿定律在直线运动中的应用.files/image320.gif)
(3)当人奔跑至右端时,人的速度%20牛顿定律在直线运动中的应用.files/image322.gif) ,木板的速度
,木板的速度%20牛顿定律在直线运动中的应用.files/image324.gif) ;人抱住木柱的过程中,系统所受的合外力远小于相互作用的内力,满足动量守恒条件,有:
;人抱住木柱的过程中,系统所受的合外力远小于相互作用的内力,满足动量守恒条件,有:
%20牛顿定律在直线运动中的应用.files/image326.gif) (其中
(其中%20牛顿定律在直线运动中的应用.files/image328.gif) 为二者共同速度)
为二者共同速度)
代入数据得%20牛顿定律在直线运动中的应用.files/image330.gif) ,方向与人原来运动方向一致;
,方向与人原来运动方向一致;
以后二者以%20牛顿定律在直线运动中的应用.files/image330.gif) 为初速度向右作减速滑动,其加速度大小为
为初速度向右作减速滑动,其加速度大小为%20牛顿定律在直线运动中的应用.files/image333.gif) ,故木板滑行的距离为
,故木板滑行的距离为%20牛顿定律在直线运动中的应用.files/image335.gif) 。
。
14. 解析:(1)从图中可以看出,在t=2s内运动员做匀加速直线运动,其加速度大小为
%20牛顿定律在直线运动中的应用.files/image337.gif) =
=
设此过程中运动员受到的阻力大小为f,根据牛顿第二定律,有mg-f=ma
得 f=m(g-a)=80×(10-8)N=160N
(2)从图中估算得出运动员在14s内下落了
39.5×2×
根据动能定理,有%20牛顿定律在直线运动中的应用.files/image339.gif)
所以有 %20牛顿定律在直线运动中的应用.files/image341.gif) =(80×10×158-
=(80×10×158-%20牛顿定律在直线运动中的应用.files/image343.gif) ×80×62)J≈1.25×105J
×80×62)J≈1.25×105J
(3)14s后运动员做匀速运动的时间为
%20牛顿定律在直线运动中的应用.files/image345.gif) s=57s
s=57s
运动员从飞机上跳下到着地需要的总时间
t总=t+t′=(14+57)s=71s
15. 13、解析:(1)取竖直向下的方向为正方向。
球与管第一次碰地前瞬间速度%20牛顿定律在直线运动中的应用.files/image347.gif) ,方向向下。
,方向向下。
碰地的瞬间管的速度%20牛顿定律在直线运动中的应用.files/image349.gif) ,方向向上;球的速度
,方向向上;球的速度%20牛顿定律在直线运动中的应用.files/image351.gif) ,方向向下,
,方向向下,
球相对于管的速度%20牛顿定律在直线运动中的应用.files/image353.gif) ,方向向下。
,方向向下。
碰后,管受重力及向下的摩擦力,加速度a管=
球受重力及向上的摩擦力,加速度a球=
球相对管的加速度a相=
取管为参照物,则球与管相对静止前,球相对管下滑的距离为:
%20牛顿定律在直线运动中的应用.files/image355.gif)
要满足球不滑出圆管,则有%20牛顿定律在直线运动中的应用.files/image357.gif) 。
。
(2)设管从碰地到它弹到最高点所需时间为t1(设球与管在这段时间内摩擦力方向不变),则:%20牛顿定律在直线运动中的应用.files/image359.gif)
设管从碰地到与球相对静止所需时间为t2,%20牛顿定律在直线运动中的应用.files/image361.gif)
因为t1 >t2,说明球与管先达到相对静止,再以共同速度上升至最高点,设球与管达到相对静止时离地高度为h’,两者共同速度为v’,分别为:
%20牛顿定律在直线运动中的应用.files/image363.gif)
%20牛顿定律在直线运动中的应用.files/image365.gif)
然后球与管再以共同速度v’作竖直上抛运动,再上升高度h’’为
%20牛顿定律在直线运动中的应用.files/image367.gif)
因此,管上升最大高度H’=h’+h’’=%20牛顿定律在直线运动中的应用.files/image369.gif)
(3)当球与管第二次共同下落时,离地高为%20牛顿定律在直线运动中的应用.files/image369.gif) ,球位于距管顶
,球位于距管顶%20牛顿定律在直线运动中的应用.files/image371.gif) 处,同题(1)可解得在第二次反弹中发生的相对位移。
处,同题(1)可解得在第二次反弹中发生的相对位移。
16. 解析:(1)小球最后静止在水平地面上,在整个运动过程中,空气阻力做功使其机械能减少,设小球从开始抛出到最后静止所通过的路程S,有 fs=mv02/2 已知 f =0.6mg 代入算得: s= 5
v02/(
(2)第一次上升和下降:设上升的加速度为a11.上升所用的时间为t11,上升的最大高度为h1;下降的加速度为a12,下降所用时间为t12.
上升阶段:F合=mg+f =1.6 mg
由牛顿第二定律:a11 =
根据:vt=v0-a11t11, vt=0
得:v0=l.6gt11, 所以t11= 5 v0/(
下降阶段:a12=(mg-f)/m=
由h1= a11t112/2 和 h2= a12t122/2 得:t12=2t11=5 v0/(
所以上升和下降所用的总时间为:T1=t11+t12=3t11= 15 v0/(
第二次上升和下降,以后每次上升的加速度都为a11,下降的加速度都为a12;设上升的初速度为v2,上升的最大高度为h2,上升所用时间为t21,下降所用时间为t22
由v22=
上升阶段:v2=a11t21 得:t21= v2/
a11= 5 v0/(
下降阶段: 由 h2= a11t212/2 和h2= a12t222/2 得t22=2t21
所以第二次上升和下降所用总时间为:T2=t21+t22=3t21=15 v0/(
第三次上升和下降,设上升的初速度为v3,上升的最大高度为h3,上升所用时间为t31,下降所用时间为t32
由 v32=
上升阶段:v3=a11t
下降阶段:由 h3= a11t312/2 和h3= a12t322/2 得:t32=2t31
所以第三次上升和下降所用的总时间为:T3=t31+t32=3t31=15 v0/(
同理,第n次上升和下降所用的总时间为: Tn=%20牛顿定律在直线运动中的应用.files/image373.gif)
所以,从抛出到落地所用总时间为: T=15 v0/(
 C.(选修模块 3 一 5 )
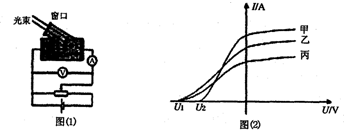
C.(选修模块 3 一 5 ) ( l )在光电效应实验中,小明同学用同一实验装置(如图 l )在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图( 2 )所示.则
( A )乙光的频率小于甲光的频率 ( B )甲光的波长大于丙光的波长 ( C )丙光的光子能量小于甲光的光子能量 ( D )乙光对应的光电子最大初动能小于丙光的光电子最大初动能
( 2 )用光照射某金属,使它发生光电效应现象,若增加该入射光的强度,则单位时间内从铝板表面逸出的光电子数
( 3 )用加速后动能为Ek0的质子:
1 1 |
4 2 |
(1)下列说法正确的是
A.原子核内部某个中子转变为质子和电子,产生的电子从原子核中发射出来,这就是β衰变
B.比结合能小的原子核结合成或分解成比结合能大的原子核时一定吸收核能
C.根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动速度减小.
D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性.
(2)现用如图1下列几种能量的光子的光照射处于基态的氢原子,A:10.25eV、B:12.09eV、C:12.45eV,则能被氢原子吸收的光子是

(3)如图2(a)所示,在水平光滑轨道上停着甲、乙两辆实验小车,甲车系一穿过打点计时器的纸带,当甲车受到水平向右的瞬时冲量时,随即启动打点计时器,甲车运动一段距离后,与静止的乙车发生正碰并粘在一起运动,纸带记录下碰撞前甲车和碰撞后两车运动情况如图2(b)所示,电源频率为50Hz,求:甲、乙两车的质量比m甲:m乙.
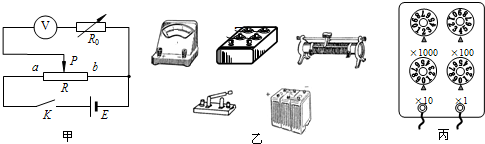
(1)试将如图乙所给实验仪器按实验电路连成测量电路.
(2)在测量时,可供选择的实验步骤有:
A.闭合开关K;
B.将电阻箱R0的阻值调到最大;
C.将电阻箱R0的阻值调到零;
D.调节电阻箱R0的阻值使电压表的指针指示1.5V,记下此时R0的值;
E.调节变阻器R的滑动片P,使电压表的指针指示3.0V;
F.把变阻器R的滑动片P滑到a端;
G.把变阻器R的滑动片P滑到b端;
H.断开开关K;
把必要的合理步骤选出来,按操作顺序将字母代号填在下面横线上
(3)若在步骤D中读出R0的阻值为如图丙所示位置,则电压表的电阻为
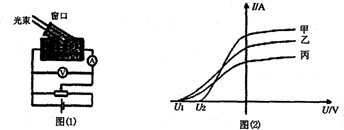
( l )在光电效应实验中,小明同学用同一实验装置(如图 l )在甲、乙、丙三种光的照射下得到了三条电流表与电压表读数之间的关系曲线,如图( 2 )所示.则
( A )乙光的频率小于甲光的频率 ( B )甲光的波长大于丙光的波长 ( C )丙光的光子能量小于甲光的光子能量 ( D )乙光对应的光电子最大初动能小于丙光的光电子最大初动能
( 2 )用光照射某金属,使它发生光电效应现象,若增加该入射光的强度,则单位时间内从铝板表面逸出的光电子数______,从表面逸出的光电子的最大动量大小______(选填“增加”、“减小”或“不变,')
( 3 )用加速后动能为Ek0的质子:
| 11 |
| 42 |
(1)下列说法正确的是______
A.原子核内部某个中子转变为质子和电子,产生的电子从原子核中发射出来,这就是β衰变
B.比结合能小的原子核结合成或分解成比结合能大的原子核时一定吸收核能
C.根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子的运动速度减小.
D.德布罗意在爱因斯坦光子说的基础上提出物质波的概念,认为一切物体都具有波粒二象性.
(2)现用如图1下列几种能量的光子的光照射处于基态的氢原子,A:10.25eV、B:12.09eV、C:12.45eV,则能被氢原子吸收的光子是______(填序号),氢原子吸收该光子后可能产生______种频率的光子.氢原子能级图为:

(3)如图2(a)所示,在水平光滑轨道上停着甲、乙两辆实验小车,甲车系一穿过打点计时器的纸带,当甲车受到水平向右的瞬时冲量时,随即启动打点计时器,甲车运动一段距离后,与静止的乙车发生正碰并粘在一起运动,纸带记录下碰撞前甲车和碰撞后两车运动情况如图2(b)所示,电源频率为50Hz,求:甲、乙两车的质量比m甲:m乙.
查看习题详情和答案>>