摘要:假设在圆上存在异于的点.使
网址:http://m.1010jiajiao.com/timu_id_486586[举报]
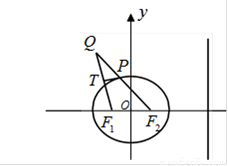
已知椭圆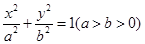 的左、右焦点分别是
的左、右焦点分别是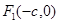 、
、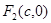 ,离心率为
,离心率为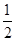 ,椭圆上的动点
,椭圆上的动点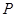 到直线
到直线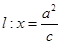 的最小距离为2,延长
的最小距离为2,延长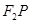 至
至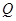 使得
使得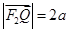 ,线段
,线段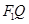 上存在异于
上存在异于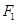 的点
的点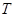 满足
满足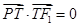 .
.
(1) 求椭圆的方程;
(2)
求点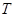 的轨迹
的轨迹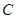 的方程;
的方程;
(3)
求证:过直线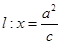 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与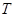 的轨迹
的轨迹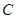 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.
查看习题详情和答案>>
(09年江苏百校样本分析)(15分)在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的圆心在第二象限,在
的圆心在第二象限,在![]() 轴上截得的弦长为4且与直线
轴上截得的弦长为4且与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若圆![]() 上存在异于原点的点
上存在异于原点的点![]() ,使点
,使点![]() 到椭圆右焦点
到椭圆右焦点![]() 的距离等于线段
的距离等于线段![]() 的长,请求出点
的长,请求出点![]() 的坐标.
的坐标.
 分别为椭圆
分别为椭圆 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是  B.
B. C.
C.
 D.
D.
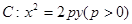 和点
和点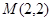 ,.斜率为
,.斜率为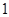 的直线与抛物线
的直线与抛物线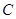 相交不同的两个点
相交不同的两个点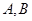 .若点
.若点 恰好为
恰好为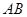 的中点.
的中点.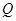 ,使得经过点
,使得经过点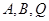 的圆和抛物线
的圆和抛物线 :
: 和点
和点 ,若抛物线
,若抛物线 、
、 满足
满足 .
. 的取值范围;
的取值范围; 时,抛物线
时,抛物线 的点
的点 ,使得经过
,使得经过 三点的圆和抛物线
三点的圆和抛物线