设函数f（x）=lnx，g（x）=ax+，函数f（x）的图像与x轴的交点也在函数g（x）的图像上，且在此点处f（x）与g（x）有公切线.[来源:学。科。网]

（Ⅰ）求a、b的值； 

（Ⅱ）设x>0，试比较f（x）与g（x）的大小.[来源:学,科,网Z,X,X,K]

【解析】第一问解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

第二问，由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

解：因为f（x）=lnx，g（x）=ax+

则其导数为

由题意得，

（11）由（I）可知，令。

∵，  …………8分

∴是（0，+∞）上的减函数，而F（1）=0，            …………9分

∴当时，，有；当时，，有；当x=1时，，有

已知数列的前项和为，且 (N^*),其中．

(Ⅰ) 求的通项公式；

(Ⅱ) 设 (N^*).

①证明： ；

② 求证：.

【解析】本试题主要考查了数列的通项公式的求解和运用。运用关系式，表示通项公式，然后得到第一问，第二问中利用放缩法得到，②由于，

所以利用放缩法，从此得到结论。

解：(Ⅰ)当时，由得.  ……2分

若存在由得，

从而有，与矛盾，所以.

从而由得得.  ……6分

 (Ⅱ)①证明：

证法一：∵∴

∴ 

∴.…………10分

证法二：，下同证法一.           ……10分

证法三：（利用对偶式）设，，

则.又，也即，所以，也即，又因为，所以.即

                    ………10分

证法四：（数学归纳法）①当时, ,命题成立;

   ②假设时,命题成立,即,

   则当时,

    即

即

故当时，命题成立.

综上可知，对一切非零自然数，不等式②成立.           ………………10分

②由于，

所以，

从而.

也即

已知函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.

(1)求f(x)的解析式；

(2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

【解析】本试题主要考查了导数在研究函数中的运用。第一问，利用函数f(x)＝ax³＋bx²＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3，得到c＝－3　∴a＝1, f(x)＝x³－3x

(2)中设切点为(x₀，x₀³－3x₀)，因为过点A(2，m)，所以∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)分离参数∴m＝－2x₀³＋6x₀²－6

然后利用g(x)＝－2x³＋6x²－6函数求导数，判定单调性，从而得到要是有三解，则需要满足－6<m<2

解：(1)f′(x)＝3ax²＋2bx＋c

依题意

又f′(0)＝－3

∴c＝－3　∴a＝1　∴f(x)＝x³－3x

(2)设切点为(x₀，x₀³－3x₀)，

∵f′(x)＝3x²－3，∴f′(x₀)＝3x₀²－3

∴切线方程为y－(x₀³－3x₀)＝(3x₀²－3)(x－x₀)

又切线过点A(2，m)

∴m－(x₀³－3x₀)＝(3x₀²－3)(2－x₀)

∴m＝－2x₀³＋6x₀²－6

令g(x)＝－2x³＋6x²－6

则g′(x)＝－6x²＋12x＝－6x(x－2)

由g′(x)＝0得x＝0或x＝2

∴g(x)在(－∞，0)单调递减，(0,2)单调递增，(2，＋∞)单调递减．

∴g(x)_极小值＝g(0)＝－6，g(x)_极大值＝g(2)＝2

画出草图知，当－6<m<2时，m＝－2x³＋6x²－6有三解，

所以m的取值范围是(－6,2)．

已知函数，.

（Ⅰ）若函数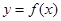依次在处取到极值.求的取值范围；

（Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

解：（1）

①

（2）不等式 ，即，即.

转化为存在实数，使对任意的，不等式恒成立.

即不等式在上恒成立.

即不等式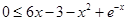在上恒成立.

设，则.

设，则，因为，有.

故在区间上是减函数。又

故存在，使得.

当时，有，当时，有.

从而在区间上递增，在区间上递减.

又[来源:]

所以当时，恒有；当时，恒有；

故使命题成立的正整数m的最大值为5

已知点为圆上的动点，且不在轴上，轴，垂足为，线段中点的轨迹为曲线，过定点任作一条与轴不垂直的直线，它与曲线交于、两点。

（I）求曲线的方程；

（II）试证明：在轴上存在定点，使得总能被轴平分

【解析】第一问中设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为

第二问中，设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　

∵，∴

确定结论直线与曲线总有两个公共点．

然后设点,的坐标分别, ，则，  

要使被轴平分，只要得到。

（1）设为曲线上的任意一点，则点在圆上，

∴，曲线的方程为．  ………………2分       

（2）设点的坐标为，直线的方程为，　　………………3分　 　

代入曲线的方程，可得　，……5分            

∵，∴，

∴直线与曲线总有两个公共点．（也可根据点M在椭圆的内部得到此结论）

………………6分

设点,的坐标分别, ，则，   

要使被轴平分，只要，            ………………9分

即，，        ………………10分

也就是，，

即，即只要　 ………………12分　 

当时，（＊）对任意的s都成立，从而总能被轴平分．

所以在x轴上存在定点，使得总能被轴平分