摘要:(Ⅱ)已知不等式对任意都成立.求实数x的取值范围. 21.
网址:http://m.1010jiajiao.com/timu_id_48201[举报]
(理)已知函数f(x)=x2+aln(x+1).
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
>
;
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln
>
恒成立.
查看习题详情和答案>>
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
| f(x1)-f(x2) |
| x1-x2 |
| 5 |
| 2 |
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln
| n+1 |
| n |
| n-1 |
| n3 |
(理)已知函数f(x)=x2+aln(x+1).
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有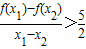 ;
;
(3)是否存在最小的正整数N,使得当n≥N时,不等式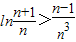 恒成立.
恒成立.
查看习题详情和答案>>
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
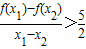 ;
;(3)是否存在最小的正整数N,使得当n≥N时,不等式
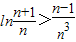 恒成立.
恒成立.查看习题详情和答案>>
(理)已知函数f(x)=x2+aln(x+1).
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有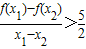 ;
;
(3)是否存在最小的正整数N,使得当n≥N时,不等式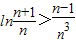 恒成立.
恒成立.
查看习题详情和答案>>
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
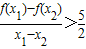 ;
;(3)是否存在最小的正整数N,使得当n≥N时,不等式
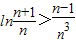 恒成立.
恒成立.查看习题详情和答案>>
(理)已知函数f(x)=x2+aln(x+1).
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
>
;
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln
>
恒成立.
查看习题详情和答案>>
(1)若函数f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(2)证明:a=1时,对于任意的x1,x2∈[1,+∞),且x1≠x2,都有
| f(x1)-f(x2) |
| x1-x2 |
| 5 |
| 2 |
(3)是否存在最小的正整数N,使得当n≥N时,不等式ln
| n+1 |
| n |
| n-1 |
| n3 |
已知数列{an}对于任意p,q∈N*,都有ap+aq=ap+q,且a1=2.
(1)求an的表达式;
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值;
(3)设An为数列{
}的前n项积,是否存在实数a,使得不等式An
<a-
对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
(1)求an的表达式;
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值;
(3)设An为数列{
| an-1 |
| an |
| an+1 |
| 3 |
| 2a |