摘要：解:(1)由.当时,原二项式为,由,则系数最大的项为
网址：http://m.1010jiajiao.com/timu_id_481214[举报]
（本小题满分12分）已知函数
（I）若函数
在区间
上存在极值，求实数a的取值范围；
（II）当
时，不等式
恒成立，求实数k的取值范围.
（Ⅲ）求证：解：（1）
，其定义域为
，则
令
，
则
，
当
时，
；当
时，
在（0，1）上单调递增，在
上单调递减，
即当时，函数取得极大值. （3分）
函数在区间
上存在极值，
，解得
（4分）
（2）不等式，即
令
（6分）
令
，则
，
，即
在
上单调递增， （7分）
，从而
，故
在上单调递增， （7分）
（8分）
（3）由（2）知，当时，
恒成立，即
，
令
，则
， （9分）
（10分）
以上各式相加得，
即
，
即
（12分）
。
查看习题详情和答案>>
.如图，由编号
，
，…，
，…（
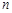且
）的圆柱自下而上组成．其中每一个圆柱的高与其底面圆的直径相等，且对于任意两个相邻圆柱，上面圆柱的高是下面圆柱的高的一半．若编号1的圆柱的高为
，则所有圆柱的体积的和为_______________（结果保留
）．
查看习题详情和答案>>
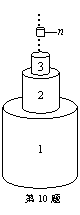如图，由编号
，
，…，
，…（
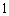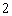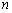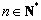且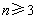
）的圆柱自下而上组成．其中每一个圆柱的高与其底面圆的直径相等，且对于任意两个相邻圆柱，上面圆柱的高是下面圆柱的高的一半．若编号1的圆柱的高为
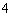，则所有圆柱的体积
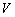为 （结果保留
）．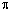