摘要:设f(x)=则f(x)的连续区间为A.(0.2) B.(0.1)C. D.(1.2)
网址:http://m.1010jiajiao.com/timu_id_481096[举报]
难点磁场
解:(1) f(x)=3,
f(x)=3,  f(x)=-1,所以
f(x)=-1,所以 f(x)不存在,所以f(x)在x=-1处不连续,
f(x)不存在,所以f(x)在x=-1处不连续,
但 f(x)=f(-1)=-1,
f(x)=f(-1)=-1,  f(x)≠f(-1),所以f(x)在x=-1处右连续,左不连续
f(x)≠f(-1),所以f(x)在x=-1处右连续,左不连续
 f(x)=3=f(1),
f(x)=3=f(1),  f(x)不存在,所以
f(x)不存在,所以 f(x)不存在,所以f(x)在x=1不连续,但左连续,右不连续.
f(x)不存在,所以f(x)在x=1不连续,但左连续,右不连续.
(2)f(x)中,区间(-∞,-1),[-1,1],(1,5]上的三个函数都是初等函数,因此f(x)除不连续点x=±1外,再也无不连续点,所以f(x)的连续区间是(-∞,-1),[-1,1]和(1,5 .
.
歼灭难点训练
答案:A
即f(x)在x=1点不连续,显知f(x)在(0,1)和(1,2)连续.
答案:C
(1)  f(x)=-1,
f(x)=-1,  f(x)=1,所以
f(x)=1,所以 f(x)不存在,故f(x)在x=0处不连续.
f(x)不存在,故f(x)在x=0处不连续.
(2)f(x)在(-∞,+∞)上除x=0外,再无间断点,由(1)知f(x)在x=0处右连续,所以f(x)在[
-1,0]上是不连续函数,在[0,1]上是连续函数.
(2)要使f(x)在(-∞,+∞)内处处连续,只要f(x)在x=0连续, f(x)
f(x)
 f(x)=
f(x)= (a+bx)=a,因为要f(x)在x=0处连续,只要
(a+bx)=a,因为要f(x)在x=0处连续,只要 f(x)=
f(x)=  f(x)
f(x)
7.证明:设f(x)=a0x3+a1x2+a2x+a3,函数f(x)在(-∞,+∞)连续,且x→+∞时,f(x)→+∞;x→-∞时,f(x)→-∞,所以必存在a∈(-∞,+∞),b∈(-∞,?+∞),使f(a)?f(b)<0,所以f(x)的图象至少在(a,b)上穿过x轴一次,即f(x)=0至少有一实根.
8.解:不连续点是x=1,连续区间是(-∞,1),(1,+∞)













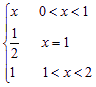 则f(x)的连续区间为( )
则f(x)的连续区间为( ) 则f(x)的连续区间为
则f(x)的连续区间为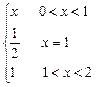 则f(x)的连续区间为( )
则f(x)的连续区间为( ) 则f(x)的连续区?间为( )
则f(x)的连续区?间为( )