摘要:考查曲线方程与点的轨迹曲线的方程或点的轨迹是高考解答题的命题对象.其命题方式还是延续传统.即放在解析几何解答题的第一小题.但由于参数方程以作为一块独立的内容放在选修1B模块中.因此与之相关的求轨迹的参数法.交轨法等方法基本不作要求.因此要重点掌握求曲线方程或点的轨迹的定义法.直接法.待定系数法.相关点法等基本方法.
网址:http://m.1010jiajiao.com/timu_id_480139[举报]
平面内与两定点 、
、
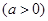 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上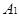 、
、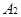 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
查看习题详情和答案>>
平面内与两定点 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
查看习题详情和答案>>
已知动点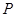 与平面上两定点
与平面上两定点 连线的斜率的积为定值
连线的斜率的积为定值 .
.
(1)试求动点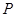 的轨迹方程
的轨迹方程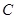 ;
;
(2)设直线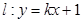 与曲线
与曲线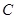 交于M.N两点,当
交于M.N两点,当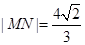 时,求直线
时,求直线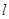 的方程.
的方程.
【解析】本试题主要是考查了轨迹方程的求解以及直线与椭圆位置关系的运用。
查看习题详情和答案>>
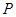 与平面上两定点
与平面上两定点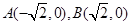 连线的斜率的积为定值
连线的斜率的积为定值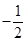 .
.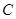 ;
;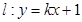 与曲线
与曲线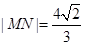 时,求直线
时,求直线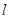 的方程.
的方程. 与平面上两定点
与平面上两定点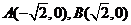 连线的斜率的积为定值
连线的斜率的积为定值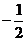 .
. ;
; 与曲线
与曲线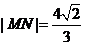 时,求直线
时,求直线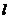 的方程.
的方程.