摘要:圆锥曲线的定义与性质是本节内容的基石.高考所考题目都会涉及.在2008年高考中.考查定义与性质的有上海卷理科第10题.山东卷文科第13题.上海卷文科第6.12题.山东卷理科第10题.海南.宁夏卷理科第11题.与未进行课改的地区相比.新课程区高考中对离心率的考查热度有所下降.仅有江苏卷第12题.
网址:http://m.1010jiajiao.com/timu_id_480138[举报]
(本小题满分14分)
如图,直线 和
和 相交于点
相交于点 且
且 ,点
,点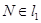 .以
.以 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到 的距离与到点
的距离与到点 的距离相等.若
的距离相等.若 为锐角三角形,
为锐角三角形, ,
, ,且
,且 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点 在曲线段C上,直线
在曲线段C上,直线 ,求直线
,求直线 被圆
被圆 截得的弦长的取值范围.
截得的弦长的取值范围.

查看习题详情和答案>>
(本小题满分10分)
选修4-4:坐标系与参数方程
已知在直角坐标系 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左,右焦点.
的左,右焦点.
(Ⅰ)以原点为极点、 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线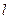 的极坐标方程;
的极坐标方程;
(Ⅱ)在(I)的条件下,设直线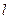 与圆锥曲线
与圆锥曲线 交于
交于 两点,求弦
两点,求弦 的长.
的长.
(本小题满分10分)
已知在直角坐标系 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
,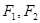 是圆锥曲线
是圆锥曲线 的左,右焦点.
的左,右焦点.
(Ⅰ)以原点为极点、 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(Ⅱ)在(I)的条件下,设直线 与圆锥曲线
与圆锥曲线 交于
交于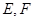 两点,求弦
两点,求弦 的长.
的长.
查看习题详情和答案>>
 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为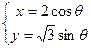 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线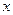 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;[来源:学科网ZXXK]
的极坐标方程;[来源:学科网ZXXK] 两点,求弦
两点,求弦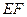 的长.
的长.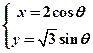 (
(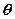 是参数)和定点
是参数)和定点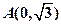 ,
,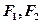 是圆锥曲线的左、右焦点。
是圆锥曲线的左、右焦点。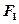 垂直于直线
垂直于直线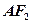 的直
的直 线l的参数方程;
线l的参数方程;