摘要:解:(1)s与之间的函数关系式是: ,(2)与图③相对应的P点的运动路径是: ,P点出发 秒首次到达点B,(3)写出当3≤s≤8时.y与s之间的函数关系式.并在图③中补全函数图象.
网址:http://m.1010jiajiao.com/timu_id_474627[举报]
某车间的甲、乙两名工人分别同时生产 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题: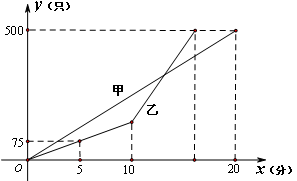
(1)甲每分钟生产零件_______只;乙在提高生产速度之前已生产了零件_______只;
(2)若乙提高速度后,乙的生产速度是甲的 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;
(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
某车间的甲、乙两名工人分别同时生产 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件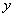 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:

(1)甲每分钟生产零件_______只;乙在提高生产速度之前已生产了零件_______只;
(2)若乙提高速度后,乙的生产速度是甲的 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件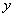 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;
(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
查看习题详情和答案>>
某车间的甲、乙两名工人分别同时生产 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:

(1)甲每分钟生产零件_______只;乙在提高生产速度之前已生产了零件_______只;
(2)若乙提高速度后,乙的生产速度是甲的 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;
(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(1)甲每分钟生产零件_______只;乙在提高生产速度之前已生产了零件_______只;
(2)若乙提高速度后,乙的生产速度是甲的
 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
已知二次函数y=ax2+bx+c(a≠0)自变量x与函数值y之间满足下列数量关系:
(1)观察表中数据,当x=6时,y的值是 ;
(2)这个二次函数与x轴的交点坐标是 ;
(3)代数式
+
+(a+b+c)(a-b+c)的值是 ;
(4)若s、t是两个不相等的实数,当s≤x≤t时,二次函数y=ax2+bx+c(a≠0)有最小值0和最大值24,那么经过点(s+1,t+1)的反比例函数解析式是 .
查看习题详情和答案>>
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 24 | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
(2)这个二次函数与x轴的交点坐标是
(3)代数式
-b+
| ||
| 2a |
-b-
| ||
| 2a |
(4)若s、t是两个不相等的实数,当s≤x≤t时,二次函数y=ax2+bx+c(a≠0)有最小值0和最大值24,那么经过点(s+1,t+1)的反比例函数解析式是
已知二次函数y=ax2+bx+c(a≠0)自变量x与函数值y之间满足下列数量关系:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 24 | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
(2)这个二次函数与x轴的交点坐标是______;
(3)代数式
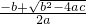 +
+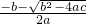 +(a+b+c)(a-b+c)的值是______;
+(a+b+c)(a-b+c)的值是______;(4)若s、t是两个不相等的实数,当s≤x≤t时,二次函数y=ax2+bx+c(a≠0)有最小值0和最大值24,那么经过点(s+1,t+1)的反比例函数解析式是______. 查看习题详情和答案>>