摘要:所以点P的坐标为(2.2)
网址:http://m.1010jiajiao.com/timu_id_474589[举报]
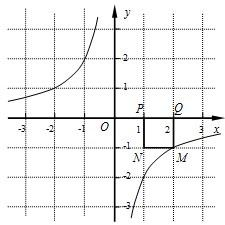 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-| 2 |
| x |
(1)如图所示,若反比例函数解析式为y=-
| 2 |
| x |
(2)请你通过改变P点坐标,对直线M1M的解析式y﹦kx+b进行探究可得k﹦
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标. 查看习题详情和答案>>
(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2:00~2:15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
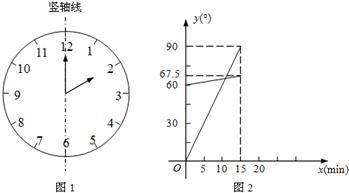
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7:30~8:00之间,时针与分针互相垂直的时刻是多少? 查看习题详情和答案>>
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.

(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7:30~8:00之间,时针与分针互相垂直的时刻是多少? 查看习题详情和答案>>
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=- 的图象上。小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限。
的图象上。小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限。
 的图象上。小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限。
的图象上。小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限。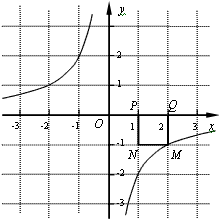
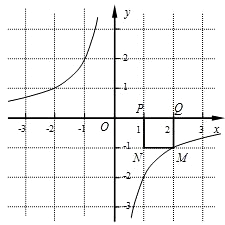
(1)如图所示,若反比例函数解析式为y=-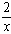 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是____。
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是____。
(2)请你通过改变P点坐标,对直线M1M的解析式y=kx+b进行探究可得k=______,若点P的坐标为(m,0)时,则b=______;
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标。
查看习题详情和答案>>
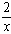 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是____。
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是____。(2)请你通过改变P点坐标,对直线M1M的解析式y=kx+b进行探究可得k=______,若点P的坐标为(m,0)时,则b=______;
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标。
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=﹣ 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
(1)如图所示,若反比例函数解析式为y=﹣ ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是 .
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是 .
(2)请你通过改变P点坐标,对直线M1M的解析式y﹦kx+b进行探究可得k﹦_________,若点P的坐标为(m,0)时,则b﹦_________;
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.(1)如图所示,若反比例函数解析式为y=﹣
 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是 .
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是 .(2)请你通过改变P点坐标,对直线M1M的解析式y﹦kx+b进行探究可得k﹦_________,若点P的坐标为(m,0)时,则b﹦_________;
(3)依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y = ![]() 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
(1)如图所示,若反比例函数解析式为y= ![]() ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
(2) 请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦ ▲ , 若点P的坐标为(m,0)时,则b﹦ ▲ ;
(3) 依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
 |
查看习题详情和答案>>