摘要:(2)由题意.可得:.
网址:http://m.1010jiajiao.com/timu_id_474525[举报]
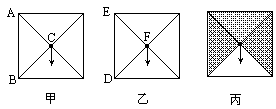
已知:如图①,正方形ABCD的边长是a,正方形AEFG的边长是b,且点F在AD上,连接DB,BF,(以下问题的结果可用a,b表示).
(1)观察计算:△DBF的面积S=
(2)图形变式:
将图①中的正方形AEFG绕点A顺时针方向旋转45°得到图②,其他条件不变,请你求出图②中△DBF的面积S;
(3)探究发现:
当a>2b时,若把图①中的正方形AEFG绕点A旋转任意角度,在旋转过程中,△DBF的面积S是否能达到最大值、最小值?如果能达到,请画出图形,并求出最大值、最小值;如果达不到,请说明理由.(图③可用来画图).
 查看习题详情和答案>>
查看习题详情和答案>>
(1)观察计算:△DBF的面积S=
(2)图形变式:
将图①中的正方形AEFG绕点A顺时针方向旋转45°得到图②,其他条件不变,请你求出图②中△DBF的面积S;
(3)探究发现:
当a>2b时,若把图①中的正方形AEFG绕点A旋转任意角度,在旋转过程中,△DBF的面积S是否能达到最大值、最小值?如果能达到,请画出图形,并求出最大值、最小值;如果达不到,请说明理由.(图③可用来画图).
 查看习题详情和答案>>
查看习题详情和答案>>
已知:如图①,正方形ABCD的边长是a,正方形AEFG的边长是b,且点F在AD上,连接DB,BF,(以下问题的结果可用a,b表示).
(1)观察计算:△DBF的面积S=______
(2)图形变式:
将图①中的正方形AEFG绕点A顺时针方向旋转45°得到图②,其他条件不变,请你求出图②中△DBF的面积S;
(3)探究发现:
当a>2b时,若把图①中的正方形AEFG绕点A旋转任意角度,在旋转过程中,△DBF的面积S是否能达到最大值、最小值?如果能达到,请画出图形,并求出最大值、最小值;如果达不到,请说明理由.(图③可用来画图).

查看习题详情和答案>>
解:根据题意,在平面直角坐标系中描出各点,可知四边形ABCD是矩形.由图形知,矩形的中心点E(5,3).
由题意知,直线y=mx-3m+2必过中心点E,所以有
3=m×5-3m+2,解得m=![]() .
.