摘要：(Ⅱ)解法一: ------ 5分
网址：http://m.1010jiajiao.com/timu_id_472953[举报]
（2012•惠州模拟）某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级：1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为x，价格满意度为y）．
（1）求高二年级共抽取学生人数；
（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；
（3）为提高食堂服务质量，现从x＜3且2≤y＜4的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率．
查看习题详情和答案>>
人数 y x |
价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 |
1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；
（3）为提高食堂服务质量，现从x＜3且2≤y＜4的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率．
一个单位有职工160人，其中业务人员96人，管理人员40人，后勤服务人员24人，为了了解职工的工作情况，要从中抽取一个容量为20的样本，有下述三种方法：
①将160人从1～160编号，然后用白纸做成从1～160号的160个签放入箱内搅匀，从中抽取20个签，与签号相对应的20人被选出；
②将160人从1～160编号，按编号顺序分成20组，每组8人，号码分别为1～8号、9～16号、…、153～160号，先从第1组中用抽签方法抽出k（0＜k＜9）号，其余组的（k+8n）号（n=1，2，…，19）亦被抽到，如此抽到20人；
③按20：160=1：8的比例，从业务人员中抽取12人，管理人员中抽取5人，后勤服务人员中抽取3人．都用随机数表法从各类人员中抽取所需的人数，他们合在一起恰好是20人．
上述三种抽样方法中，按简单随机抽样法、分层抽样法、系统抽样的依次是（ ）
查看习题详情和答案>>
①将160人从1～160编号，然后用白纸做成从1～160号的160个签放入箱内搅匀，从中抽取20个签，与签号相对应的20人被选出；
②将160人从1～160编号，按编号顺序分成20组，每组8人，号码分别为1～8号、9～16号、…、153～160号，先从第1组中用抽签方法抽出k（0＜k＜9）号，其余组的（k+8n）号（n=1，2，…，19）亦被抽到，如此抽到20人；
③按20：160=1：8的比例，从业务人员中抽取12人，管理人员中抽取5人，后勤服务人员中抽取3人．都用随机数表法从各类人员中抽取所需的人数，他们合在一起恰好是20人．
上述三种抽样方法中，按简单随机抽样法、分层抽样法、系统抽样的依次是（ ）
（2012•开封二模）甲乙两个学校高三年级分别有1100人，1000人，为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样的方法从两个学校一共抽取了105名学生的数学成绩，并作出了频数分布统计表如下，规定考试成绩[120，150]内为优秀，
甲校：
乙校：
（1）计算x，y的值；
（2）由以上统计数据填写右面2×2列联表，若按是否优秀来判断，是否有97.5%的把握认为两个学校的数学成绩有差异．
（3）根据抽样结果分别估计甲校和乙校的优秀率；若把频率作为概率，现从乙校学生中任取3人，求优秀学生人数ξ的分布列和数学期望．
附：k2=
查看习题详情和答案>>
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 2 | 3 | 10 | 15 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 15 | 10 | y | 3 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 1 | 2 | 9 | 8 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 10 | 10 | y | 3 |
（2）由以上统计数据填写右面2×2列联表，若按是否优秀来判断，是否有97.5%的把握认为两个学校的数学成绩有差异．
（3）根据抽样结果分别估计甲校和乙校的优秀率；若把频率作为概率，现从乙校学生中任取3人，求优秀学生人数ξ的分布列和数学期望．
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P（K2＞K） | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
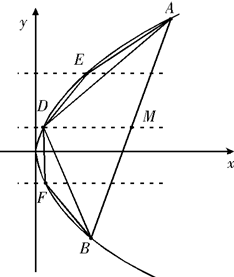（2007•浦东新区二模）已知抛物线C：y2=2px（p＞0）上横坐标为4的点到焦点的距离为5．（1）求抛物线C的方程．
（2）设直线y=kx+b（k≠0）与抛物线C交于两点A（x1，y1），B（x2，y2），且|y1-y2|=a（a＞0），M是弦AB的中点，过M作平行于x轴的直线交抛物线C于点D，得到△ABD；再分别过弦AD、BD的中点作平行于x轴的直线依次交抛物线C于点E，F，得到△ADE和△BDF；按此方法继续下去．
解决下列问题：
①求证：a2=
| 16(1-kb) | k2 |
②计算△ABD的面积S△ABD；
③根据△ABD的面积S△ABD的计算结果，写出△ADE，△BDF的面积；请设计一种求抛物线C与线段AB所围成封闭图形面积的方法，并求出此封闭图形的面积．