摘要:集合.若.则的取值范围是 .分析:题目中的两个集合可以看作是平面上的两个区域.题目要解决的是这两个区域有公共点的问题.可以借助于数形结合的方法去探究问题的答案.
网址:http://m.1010jiajiao.com/timu_id_454356[举报]
(本小题满分14分)
函数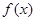 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“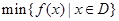 ”表示函数
”表示函数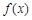 在集合D上的最小值,“
在集合D上的最小值,“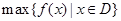 ”表示函数
”表示函数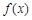 在集合D上的最大值.现设
在集合D上的最大值.现设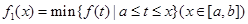 ,
,
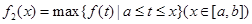 ,
,
若存在最小正整数k,使得 对任意的
对任意的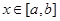 成立,则称函数
成立,则称函数
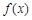 为区间
为区间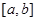 上的“第k类压缩函数”.
上的“第k类压缩函数”.
(Ⅰ) 若函数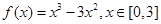 ,求
,求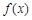 的最大值,写出
的最大值,写出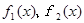 的解析式;
的解析式;
(Ⅱ) 若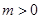 ,函数
,函数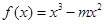 是
是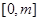 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.
查看习题详情和答案>>
(本小题满分14分)
函数![]() 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“![]() ”表示函数
”表示函数![]() 在集合D上的最小值,“
在集合D上的最小值,“![]() ”表示函数
”表示函数![]() 在集合D上的最大值.现设
在集合D上的最大值.现设![]() ,
,
![]() ,
,
若存在最小正整数k,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数
![]() 为区间
为区间![]() 上的“第k类压缩函数”.
上的“第k类压缩函数”.
(Ⅰ) 若函数![]() ,求
,求![]() 的最大值,写出
的最大值,写出![]() 的解析式;
的解析式;
(Ⅱ) 若![]() ,函数
,函数![]() 是
是![]() 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.
ks**5u
查看习题详情和答案>>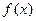 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“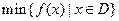 ”表示函数
”表示函数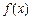 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数 ,
,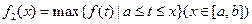 ,
,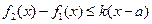 对任意的
对任意的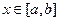 成立,则称函数
成立,则称函数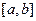 上的“第k类压缩函数”.
上的“第k类压缩函数”.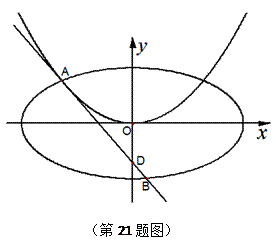
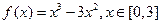 ,求
,求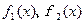 的解析式;
的解析式;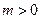 ,函数
,函数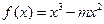 是
是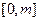 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.