网址:http://m.1010jiajiao.com/timu_id_451291[举报]
一、
二、
9.16 10.2009 11.卷.files/image133.gif) 12.
12.卷.files/image135.gif)
13.卷.files/image137.gif) 14.3
14.3 卷.files/image139.gif) 15.②③
15.②③
三、
16.解:(1)由余弦定理得: 卷.files/image141.gif)
卷.files/image143.gif)
卷.files/image145.gif) 是以角C为直角的直角三角形.……………………6分
是以角C为直角的直角三角形.……………………6分
(2)卷.files/image147.gif) 中
中
卷.files/image149.gif) ………………①
………………①
卷.files/image151.gif) ………………②
………………②
②÷①得卷.files/image153.gif) ,
,
则卷.files/image155.gif) ……………………12分
……………………12分
17.解:(1)因为卷.files/image157.gif) ……………………………………(2分)
……………………………………(2分)
卷.files/image159.gif) ……………………………………………………(4分)
……………………………………………………(4分)
卷.files/image161.gif)
所以线路信息通畅的概率为卷.files/image163.gif) 。………………………(6分)
。………………………(6分)
(2)卷.files/image083.gif) 的所有可能取值为4,5,6,7,8。
的所有可能取值为4,5,6,7,8。
卷.files/image166.gif)
卷.files/image168.gif) ……………………………………………………………(9分)
……………………………………………………………(9分)
∴卷.files/image170.gif) 的分布列为
的分布列为
卷.files/image170.gif)
4
5
6
7
8
P
卷.files/image172.gif)
卷.files/image174.gif)
卷.files/image176.gif)
卷.files/image174.gif)
卷.files/image172.gif)
…………………………………………………………………………………………(10分)
∴E卷.files/image083.gif) =4×
=4×卷.files/image172.gif) +5×
+5×卷.files/image174.gif) +6×
+6×卷.files/image176.gif) +7×
+7×卷.files/image174.gif) +8×
+8×卷.files/image172.gif) =6。……………………(12分)
=6。……………………(12分)
18.解:解法一:(1)证明:连结OC,
∵卷.files/image086.gif) ABD为等边三角形,O为BD的中点,∴AO
ABD为等边三角形,O为BD的中点,∴AO
垂直BD。………………………………………………………………(1分)
∴ AO=CO=卷.files/image022.gif) 。………………………………………………………………………(2分)
。………………………………………………………………………(2分)
在卷.files/image180.gif) AOC中,AC=
AOC中,AC=卷.files/image089.gif) ,∴AO2+CO2=AC2,
,∴AO2+CO2=AC2,
∴∠AOC=900,即AO⊥OC。
∴BD卷.files/image183.gif) OC=O,∴AO⊥平面BCD。…………………………………………………(3分)
OC=O,∴AO⊥平面BCD。…………………………………………………(3分)
(2)过O作OE垂直BC于E,连结AE,
∵AO⊥平面BCD,∴AE在平面BCD上的射影为OE。
∴AE⊥BC。
∠AEO为二面角A―BC―D的平面角。………………………………………(7分)
在Rt卷.files/image184.gif) AEO中,AO=
AEO中,AO=卷.files/image022.gif) ,OE=
,OE=卷.files/image186.gif) ,
,
卷.files/image188.gif) ∠
∠卷.files/image190.gif) ,
,
∴∠AEO=arctan2。
二面角A―BC―D的大小为arctan2。
(3)设点O到面ACD的距离为卷.files/image192.gif) ∵VO-ACD=VA-OCD,
∵VO-ACD=VA-OCD,
∴卷.files/image194.gif) 。
。
在卷.files/image184.gif) ACD中,AD=CD=2,AC=
ACD中,AD=CD=2,AC=卷.files/image089.gif) ,
,
卷.files/image197.gif) 。
。
|
卷.files/image199.jpg)
卷.files/image203.gif) 。
。卷.files/image205.gif) 。…………………(12分)
。…………………(12分)卷.files/image209.gif) =(0,0,
=(0,0,卷.files/image211.gif) )。…………………………………………(5分)
)。…………………………………………(5分)卷.files/image213.jpg)
卷.files/image217.gif) ,
,卷.files/image219.gif) 。设
。设卷.files/image221.gif) 与
与卷.files/image224.gif) ,
,卷.files/image226.gif) 。
。卷.files/image228.gif) 。…………………………………………(8分)
。…………………………………………(8分)卷.files/image230.gif) 又
又卷.files/image232.gif)
卷.files/image234.gif) 。………………………………(11分)
。………………………………(11分)卷.files/image236.gif) 与
与卷.files/image238.gif) 夹角为
夹角为卷.files/image240.gif) ,则
,则卷.files/image242.gif)
卷.files/image245.gif) ,
,卷.files/image248.gif) .
.卷.files/image250.gif) …共线,该直线过点P1(a,a),
…共线,该直线过点P1(a,a),卷.files/image252.gif) ……………………3分
……………………3分卷.files/image254.gif) 时,An是一个三角形与一个梯形面积之和(如上图所示),梯形面积是
时,An是一个三角形与一个梯形面积之和(如上图所示),梯形面积是卷.files/image256.gif)
卷.files/image258.gif)
卷.files/image260.gif)
卷.files/image262.gif) …………………………7分
…………………………7分卷.files/image264.gif)
卷.files/image266.gif) ,……………………10分
,……………………10分卷.files/image268.gif)
卷.files/image270.gif) ,
,卷.files/image272.gif) ……………………13分
……………………13分卷.files/image274.gif) ,
,卷.files/image276.gif)
卷.files/image278.gif)
卷.files/image280.gif) 为正三角形,
为正三角形,卷.files/image282.gif)
卷.files/image284.gif) ……………………2分
……………………2分卷.files/image286.gif) ),N(
),N(卷.files/image288.gif) ),
),卷.files/image290.gif) 得,
得,卷.files/image292.gif)
卷.files/image294.gif) ……………………4分
……………………4分卷.files/image296.gif) ………………6分
………………6分卷.files/image298.gif) 且满足上述方程,
且满足上述方程,卷.files/image300.gif) ………………7分
………………7分卷.files/image303.gif)
卷.files/image305.gif)
卷.files/image307.gif)
卷.files/image309.gif) …………………………9分
…………………………9分卷.files/image311.gif)
卷.files/image313.gif)
卷.files/image315.gif) ……………………10分
……………………10分卷.files/image317.gif)
卷.files/image319.gif)
卷.files/image321.gif) 面积的最大值为
面积的最大值为卷.files/image323.gif) …………………………13分
…………………………13分卷.files/image325.gif)
卷.files/image327.gif) ……………………3分
……………………3分卷.files/image329.gif)
卷.files/image331.gif) >
>卷.files/image333.gif) >
>卷.files/image335.gif) >0,
>0,卷.files/image125.gif) ≥
≥卷.files/image338.gif) ≥
≥卷.files/image340.gif) ≥
≥卷.files/image342.gif) …(5分)
…(5分)卷.files/image344.gif)
卷.files/image346.gif)
卷.files/image348.gif) ……………………7分
……………………7分卷.files/image350.gif)
卷.files/image352.gif)
卷.files/image354.gif)
卷.files/image356.gif) ,
,卷.files/image358.gif)
卷.files/image360.gif) ;………………9分
;………………9分卷.files/image362.gif)
卷.files/image364.gif) 再三式作和即得
再三式作和即得卷.files/image366.gif)
卷.files/image368.gif)
卷.files/image370.gif)
卷.files/image131.gif) ……………………13分
……………………13分 的一个焦点与抛物线
的一个焦点与抛物线 的焦点相同,离心率为2,则此双曲线的方程为
的焦点相同,离心率为2,则此双曲线的方程为



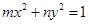 的一个焦点与抛物线
的一个焦点与抛物线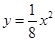 的焦点相同,离心率为2,则此双曲线的方程为
的焦点相同,离心率为2,则此双曲线的方程为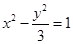
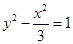
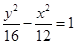
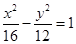
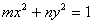 的一个焦点与抛物线
的一个焦点与抛物线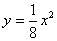 的焦点相同,离心率为2,则此双曲线
的焦点相同,离心率为2,则此双曲线