网址:http://m.1010jiajiao.com/timu_id_45089[举报]
一、 选择题(本大题共8小题,每小题5分,共40分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
D
A
B
B
D
A
C
C
二、填空题(本大题共6小题,每小题5分,有两空的小题,第一空3分,第二空2分,共30分)
(9)2 (10)y=sin(2x+
 )
(11)
)
(11)  (12)(-∞,-1)∪(-1,1) (13)16,
(12)(-∞,-1)∪(-1,1) (13)16, 
(14)72,120
三、解答题(本大题共6小题,共80分)
(15)(共13分)
解:(Ⅰ)f(x)=cos2x+2 sinxcosx-sin2x
sinxcosx-sin2x
= sin2x+cos2x……………………………………………………4分
sin2x+cos2x……………………………………………………4分
=2sin(2x+ )………………………………………………………5分
)………………………………………………………5分
∴T= , f(x)∈[-2,2] ……………………………………………7分
, f(x)∈[-2,2] ……………………………………………7分
(Ⅱ)由f( )=2,有f(
)=2,有f( )=2sin(A+
)=2sin(A+ )=2, ………………………………8分
)=2, ………………………………8分
∴sin(A+ )=1.
)=1.
∵0<A< ,∴A+
,∴A+ =
= ,即A=
,即A= .……………………………………10分
.……………………………………10分
由余弦定理a2=b2+c2-2bccosA及a2=bc,∴(b-c)2=0. ………………12分
则b=c,∴B=C= .
.
∴△ABC为等边三角形. ……………………………………………13分
(16)(共13分)
解:(Ⅰ)∵S1=a1=1,且数列{Sn}是以2为公比的等比数列,
∴Sn=2n-1.……………………………………………………………2分
又当n≥2时,an=Sn-Sn-1=2n-2(2-1)=2n-2. …………………………5分
 ∴an=
∴an= ………………………………………………7分
………………………………………………7分
(Ⅱ)a3,a5,…,a2n+1是以2为首项,以4为公比的等比数列,…………9分
∴a3+a5+…+a2n+1= …………………………11分
…………………………11分
∴a1+a3+…+a2n+1=1+ …………………………13分
…………………………13分
(17)(共14分)
方法一:
(Ⅰ)证明:连结BD交AC于E,连结ME.…………………………………1分
∵ABCD是正方形,∴E是BD的中点.∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB.………………………………………………………………………2分
又∵ME?平面ACM,SB?平面ACM, ………………………………………3分
∴SB∥平面ACM.………………………………………………………………4分
(Ⅱ)解:取AD中点F,则MF∥SA.作FQ⊥AC于Q,连结MQ. ………5分
∵SA⊥底面ABCD,∴MF⊥底面ABCD.
∴FQ为MQ在平面ABCD内的射影.
∵FQ⊥AC,
∴MQ⊥AC.
∴∠FQM为二面角D-AC-M的平面角.………………………………………7分
设SA=AB=a,在Rt△MFQ中,MF= SA=
SA= ,FQ=
,FQ= DE=
DE= a,
a,
∴tanFQM=
∴二面角D-AC-M的大小为arctan . ………………………………………9分
. ………………………………………9分
(Ⅲ)证明:由条件有DC⊥SA,DC⊥DA,∴DC⊥平面SAD,∴AM⊥DC.…………10分
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC. ………………………………………………………………11分
∴SC⊥AM.
由已知SC⊥AN,∴SC⊥平面AMN.
又SC?平面SAC,∴平面SAC⊥平面AMN. …………………………………14分
 方法二:
方法二:
解:(Ⅱ)如图,以A为坐标原点,建立空间直角坐
标系A-xyz, ……………………………5分
由SA=AB,故设AB=AD=AS=1,则
A(0,0,0),B(0,1,0),C(1,1,0),
D(1,0,0),S(0,0,1),M( ,0,
,0, ).
).
∵SA⊥底面ABCD,
 ∴
∴ 是平面ABCD的法向量,
是平面ABCD的法向量,
 =(0,0,1).
=(0,0,1).
设平面ACM的法向量为n=(x, y, z),
 =(1,1,0),
=(1,1,0),  =(
=( ),………………………………………………7分
),………………………………………………7分
 |
令x=1,则n=(1,-1,-1). …………………………………………………………8分
 ∴cos<
∴cos< , n>= = =
, n>= = =
∴二面角D-AC-M的大小为arccos .………………………………………9分
.………………………………………9分
(Ⅲ)∵ =(
=( ,0,
,0, ),
), =(-1,-1,1),…………………………………………10分
=(-1,-1,1),…………………………………………10分
∴ ?
? = -
= - +
+ =0.
=0.
∴ ⊥
⊥ .…………………………………………………………………………12分
.…………………………………………………………………………12分
又∵SC⊥AN且AN∩AM=A,
∴SC⊥平面AMN.又SC 平面SAC,
平面SAC,
∴平面SAC⊥平面AMN.…………………………………………………………14分
(18)(共12分)
解:(Ⅰ)设“这4个家庭中恰好有3个家庭订阅了A报”的事件为A,………1分
P(A)=  (0.3)3(0.7)=0.0756
…………………………………………4分
(0.3)3(0.7)=0.0756
…………………………………………4分
答:这4个家庭中恰好有3个家庭订阅了A报的概率为0.0756.
(Ⅱ)设“这4个家庭中至多有3个家庭订阅了B报”的事件为B,………5分
P(B)=1-(0.6)4=1-0.1296=0.8704…………………………………………8分
答:这4个家庭中至多有3个家庭订阅了B报的概率为0.8704.
(Ⅲ)设“这4个家庭中恰好有2个家庭A,B报都没有订阅”的事件为C, …9分
因为有30%的家庭订阅了A报,有60%的家庭订阅了B报,
有20%的家庭同时订阅了A报和B报.所以两份报纸都没有订阅的家庭
有30%.
所以P(C)=  (0.3)2(0.7)2=0.2646
…………………………………12分
(0.3)2(0.7)2=0.2646
…………………………………12分
答:这4个家庭中恰好有2个家庭A,B报都没有订阅的概率为0.2646.
注:第三问若写出两份报纸都没有订阅的家庭有30%,后面计算有误,给到10分.
(19)(共14分)
解:(Ⅰ)设抛物线S的方程为y2=2px.…………………………………………1分
由 可得2y2+py-20p=0.……………………………………3分
可得2y2+py-20p=0.……………………………………3分
由Δ>0,有p>0,或p<-160.
设B(x1,y1),C(x2,y2),则y1+y2= .
.
∴x1+x2=(5- )+(5-
)+(5- )=10-
)=10- =10+
=10+ .…………………………5分
.…………………………5分
设A(x3,y3),由△ABC的重心为F( ,0),则
,0),则
∴x3=
∵点A在抛物线S上,∴( )2=2p(
)2=2p( ),∴p=8.…………………6分
),∴p=8.…………………6分
∴抛物线S的方程为y2=16x.……………………………………………………7分
(Ⅱ)当动直线PQ的斜率存在时,设PQ的方程为y=kx+b,显然k≠0,b≠0.………
……………………………………………………………………………………8分
设P(xp, yp),Q(xQ, yQ),∵OP⊥OQ,∴kOP?kOQ=-1.
∴ ?
? =-1,∴xP xQ
+ yP yQ=0. …………………………………………10分
=-1,∴xP xQ
+ yP yQ=0. …………………………………………10分
将y=kx+b代入抛物线方程,得ky2-16y+16b=0,∴yPyQ= .
.

∵k≠0,b≠0,∴b=-16k,∴动直线方程为y=kx-16k=k(x-16).
此时动直线PQ过定点(16,0).………………………………………………12分
当直线PQ 的斜率不存在时,显然PQ⊥x轴,又OP⊥OQ,∴△POQ为等腰直角三角形.
由 得到P(16,16),Q(16,-16).
得到P(16,16),Q(16,-16).
此时直线PQ亦过点(16,0). …………………………………………………13分
综上所述,动直线PQ过定点M(16,0). ………………………………………14分
(20)(共14分)
解:(Ⅰ)由已知,可得f '(x)=2ax+b, …………………………………………1分
∴ 解之得a=
解之得a= .…………………………………………3分
.…………………………………………3分
(Ⅱ)∵ ∴
∴
由 =2×1
=2×1
 =2×2
=2×2
 =2×3
=2×3
…

累加得 =n2-n(n=2,3…).………………………………………………6分
=n2-n(n=2,3…).………………………………………………6分
∴an= (n=2,3…).
(n=2,3…).
当n=1时, ………………………………………………7分
………………………………………………7分
∴an= (n=1,2,3…).……………………………………………8分
(n=1,2,3…).……………………………………………8分
(Ⅲ)当k=1时,由已知a1=4<5显然成立;………………………………………9分
当k≥2时,ak= <
< (k≥2)……………………11分
(k≥2)……………………11分
则a1+a2+a3+…+ak<4+[(1- )+(
)+( )+…+ (
)+…+ ( )]=5-
)]=5- <5
<5
………………………………………………………………………………13分
综上,a1+a2+a3+…+ak<5(k=1,2,3…)成立. ………………………………14分
说明:其他正确解法按相应步骤给分.

 (B)
(B) (C)
(C) (D)
(D)

 (B)
(B) (C)
(C)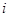 (D)
(D)