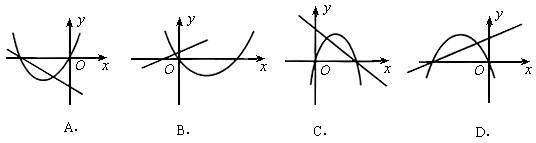摘要：例4. 在同一坐标平面内.函数与的图象只可能是( ) 解:选择支A中抛物线肯定错误.B中直线肯定错误.C中直线和抛物线不是同时正确的.故选D. 点拨:排除法就是利用一些基本概念.定理和简单的运算.通过排除容易发现错误的选择支.从而推断正确答案的方法.
网址：http://m.1010jiajiao.com/timu_id_4464352[举报]
在直角坐标平面内，二次函数图象的经过A（-1，0）、B（3，0），且过点C（0，3）．
（1）求该二次函数的解析式；
（2）若P是该抛物线上一点，且△ABC与△ABP面积相同，求P的坐标．
查看习题详情和答案>>
（1）求该二次函数的解析式；
（2）若P是该抛物线上一点，且△ABC与△ABP面积相同，求P的坐标．
在直角坐标平面内，二次函数图象的经过A（-1，0）、B（3，0），且过点C（0，3）．
（1）求该二次函数的解析式；
（2）若P是该抛物线上一点，且△ABC与△ABP面积相同，求P的坐标．
查看习题详情和答案>>
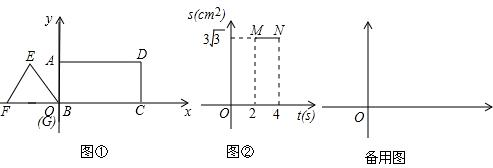
在平面直角坐标系中，矩形ABCD与等边△EFG按如图①所示放置：点B、G与坐标原点O重合，F、B、G、C在x轴上，E、A、D三点同在平行于x轴的直线上．△EFG沿x轴向右匀速移动，当点G移至与点C重合时，△EFG即停止移动．在△EFG移动过程中，与矩形ABCD的重合部分的面积S（cm2）与移动时间t（s）的一部分函数图象是线段MN如图②所示（即△EFG完全进入矩形ABCD内部时的一段函数图象）
（1）结合图②，求等边△EFG的边长和它移动的速度；
（2）求S与t的函数关系式，并在图②中补全△EFG在整个移动过程中，S与t的函数关系式的大致图象；
（3）当△EFG移动（
+1）s时，E点到达P点的位置，一开口向下的抛物线y=
x2+bx，过P、O两点且与射线AD相交于点H，与x轴相交于点Q（异于原点）．请问a是否存在取某一值或某一范围，使OQ+PH的值为定值？如果存在，求出a值或a的取值范围；如果不存在，请说明理由．
查看习题详情和答案>>
（1）结合图②，求等边△EFG的边长和它移动的速度；
（2）求S与t的函数关系式，并在图②中补全△EFG在整个移动过程中，S与t的函数关系式的大致图象；
（3）当△EFG移动（
| 3 |
| 1 |
| a |
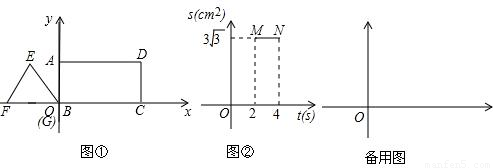
在平面直角坐标系中，矩形ABCD与等边△EFG按如图①所示放置：点B、G与坐标原点O重合，F、B、G、C在x轴上，E、A、D三点同在平行于x轴的直线上．△EFG沿x轴向右匀速移动，当点G移至与点C重合时，△EFG即停止移动．在△EFG移动过程中，与矩形ABCD的重合部分的面积S（cm2）与移动时间t（s）的一部分函数图象是线段MN如图②所示（即△EFG完全进入矩形ABCD内部时的一段函数图象）
（1）结合图②，求等边△EFG的边长和它移动的速度；
（2）求S与t的函数关系式，并在图②中补全△EFG在整个移动过程中，S与t的函数关系式的大致图象；
（3）当△EFG移动（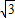
+1）s时，E点到达P点的位置，一开口向下的抛物线y=
，过P、O两点且与射线AD相交于点H，与x轴相交于点Q（异于原点）．请问a是否存在取某一值或某一范围，使OQ+PH的值为定值？如果存在，求出a值或a的取值范围；如果不存在，请说明理由．
查看习题详情和答案>>
（1）结合图②，求等边△EFG的边长和它移动的速度；
（2）求S与t的函数关系式，并在图②中补全△EFG在整个移动过程中，S与t的函数关系式的大致图象；
（3）当△EFG移动（
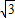+1）s时，E点到达P点的位置，一开口向下的抛物线y=，过P、O两点且与射线AD相交于点H，与x轴相交于点Q（异于原点）．请问a是否存在取某一值或某一范围，使OQ+PH的值为定值？如果存在，求出a值或a的取值范围；如果不存在，请说明理由．查看习题详情和答案>>