摘要:设a,b∈R.且a≠2,定义在区间=是奇函数. (1)求b的取值范围, 的单调性. 解 =lg 是奇函数等价于: 对任意x∈都有 式即为.由此可得 ,也即a2x2=4x2,此式对任意x∈都成立相当于a2=4,因为a≠2,所以a=-2.代入②式.得>0,即-<x<,此式对任意x∈都成立相当于-≤-b<b≤, 所以b的取值范围是(0, ]. (2)设任意的x1,x2∈.且x1<x2, 由b∈(0.].得-≤-b<x1<x2<b≤, 所以0<1-2x2<1-2x1,0<1+2x1<1+2x2, 从而f(x2)-f(x1)= 因此f内是减函数.具有单调性.
网址:http://m.1010jiajiao.com/timu_id_4463575[举报]
对定义在区间D上的函数f(x),若存在闭区间[a,b]⊆D和常数C,使得对任意的x∈[a,b]都有f(x)=C,且对任意的x∉[a,b]都有f(x)>C恒成立,则称函数f(x)为区间D上的“U型”函数.
(1)求证函数f(x)=|x-1|+|x-3|是R上的“U型”函数;
(2)设函数f(x)是(1)中的“U型”函数,若不等式|t-1|+|t-2|≤f(x)对一切t∈R恒成立,求实数t的取值范围.
(3)若函数g(x)=mx+
是区间[-2,+∞)上的“U型”函数,求实数m和n的值.
查看习题详情和答案>>
(1)求证函数f(x)=|x-1|+|x-3|是R上的“U型”函数;
(2)设函数f(x)是(1)中的“U型”函数,若不等式|t-1|+|t-2|≤f(x)对一切t∈R恒成立,求实数t的取值范围.
(3)若函数g(x)=mx+
| x2+2x+n |
设定义在区间[x1,x2]上的函数y=f(x)的图象为C,点A、B的坐标分别为(x1,f(x1)),(x2f(x2))且M(x,f(x))为图象C上的任意一点,O为坐标原点,当实数λ满足x=λx1+(1-λ)x2时,记向量
=λ
+(1-λ)
.若|
|≤k恒成立,则称函数y=f(x)在区间[x1,x2]上可在标准k下线性近似,其中k是一个确定的正数.
(Ⅰ)求证:A、B、N三点共线
(Ⅱ)设函数f(x)=x2在区间[0,1]上可的标准k下线性近似,求k的取值范围;
(Ⅲ)求证:函数g(x)=lnx在区间(em,em+1)(m∈R)上可在标准k=
下线性近似.
(参考数据:e=2.718,ln(e-1)=0.541)
查看习题详情和答案>>
| ON |
| OA |
| OB |
| MN |
(Ⅰ)求证:A、B、N三点共线
(Ⅱ)设函数f(x)=x2在区间[0,1]上可的标准k下线性近似,求k的取值范围;
(Ⅲ)求证:函数g(x)=lnx在区间(em,em+1)(m∈R)上可在标准k=
| 1 |
| 8 |
(参考数据:e=2.718,ln(e-1)=0.541)
 恒成立,则称函数y=f(x)在区间[x1,x2]上可在标准k下线性近似,其中k是一个确定的正数.
恒成立,则称函数y=f(x)在区间[x1,x2]上可在标准k下线性近似,其中k是一个确定的正数.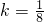 下线性近似.
下线性近似.