摘要: 据调查.某地区100万从事传统农业的农民.人均收入3 000元.为了增加农民的收入.当地政府积极引进资本.建立各种加工企业.对当地的农产品进行深加工.同时吸收当地部分农民进入加工企业工作.据估计.如果有x 万人进企业工作.那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3 000a元 . (1)在建立加工企业后.要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入.试求x的取值范围, 的条件下.当地政府应该如何引导农民.能使这100万农民的人均年收入达到最大. 解(1)由题意得 ·3 000·≥100×3 000, 即x2-50x≤0,解得0≤x≤50. 又∵x>0,∴0<x≤50. (2)设这100万农民的人均年收入为y元, 则y= =-.∴若25(a+1)≤50,即0<a≤1时.当x=25(a+1)时. ymax= 若a>1时.函数在上是增函数. ∴当x=50时.y max=×502+30(a+1) ×50+3 000=-1 500+1 500a+1 500+3 000=1 500a+3 000. 答 若0<a≤1,当x=25(a+1)时,使100万农民人均年收入最大. 若a>1,当x=50时,使100万农民的人均年收入最大.
网址:http://m.1010jiajiao.com/timu_id_4463574[举报]
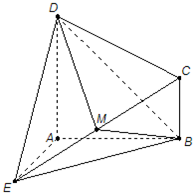 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.(Ⅰ)求证:DM⊥EB;
(Ⅱ)求二面角M-BD-A的余弦值.
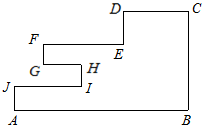 (2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )
(2008•深圳二模)一个质点从A出发依次沿图中线段到达B、C、D、E、F、G、H、I、J各点,最后又回到A(如图所示),其中:AB⊥BC,AB∥CD∥EF∥HG∥IJ,BC∥DE∥FG∥HI∥JA.欲知此质点所走路程,至少需要测量n条线段的长度,则n=( )