摘要:已知函数f(x)=log2+log2(x-1)+log2(p-x). 的定义域, 的值域. 解 有意义时.有 由①.②得x>1,由③得x<p,因为函数的定义域为非空数集.故p>1,f. =log2[] =log2[-(x-)2+] , ①当1<<p.即p>3时. 0<-(x-, ∴log2≤2log2(p+1)-2. ②当≤1.即1<p≤3时. ∵0<-(x- ∴log2<1+log2(p-1). 综合①②可知: 当p>3时.f(x)的值域是(-∞,2log2(p+1)-2]; 当1<p≤3时. f(x)的值域是(-∞,1+log2.
网址:http://m.1010jiajiao.com/timu_id_4463483[举报]
已知函数f(x)=log2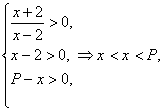 ,g(x)=log2(x-2)+log2(p-x),且p>2,设F(x)=g(x)+f(x).
,g(x)=log2(x-2)+log2(p-x),且p>2,设F(x)=g(x)+f(x).
(1)求使f(x),g(x)同时有意义的x的取值范围;
(2)F(x)是否存在最大值或最小值?若存在,则求出它的最大值与最小值.
查看习题详情和答案>>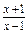 +log2(x-1)+log2(p-x).
+log2(x-1)+log2(p-x).