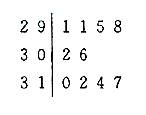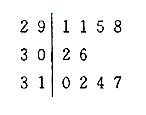摘要:已知集合M={-1,1},N={x|<2x+1<4,x∈Z},则M∩N等于 ( ) ?A.{-1,1}? B.{-1}? C.{0}? D.{-1,0} 答案?B ? 例1 已知a=,b=9.求: (1), (2) 解 (1)原式=aa=a ∵a=.∴原式=3. (2)方法一 化去负指数后解. =a+b. ∵a=.b=9.∴a+b=. 方法二 利用运算性质解. =b+a. ∵a=.b=9.∴a+b=. 例2 函数f(x)=x2-bx+c满足f=3,则f(bx)与f(cx)的大小关系是 ( ) ?A.f(bx)≤f(cx)? B.f(bx)≥f(cx) ?C.f(bx)>f(cx)? D.大小关系随x的不同而不同 答案?A? 例3 求下列函数的定义域.值域及其单调区间: =; =-()x+4()x+5. 解 (1)依题意x2-5x+4≥0, 解得x≥4或x≤1, ∴f(x)的定义域是. 令u= ∵x∈. ∴u≥0.即≥0. 而f(x)=3≥30=1, ∴函数f. ∵u=. ∴当x∈(-∞.1]时.u是减函数. 当x∈[4.+∞)时.u是增函数. 而3>1,∴由复合函数的单调性可知. f(x)=在(-∞.1]上是减函数. 在[4.+∞)上是增函数. 故f.减区间是(-∞.1]. =-()x+4()x+5 =-()2x+4()x+5, ∴函数的定义域为R.令t=()x , ∴g(t)=-t2+4t+5=-(t-2)2+9, ∵t>0,∴g2+9≤9, 等号成立条件是t=2, 即g(x)≤9,等号成立条件是()x=2.即x=-1. ∴g(x)的值域是(-∞.9]. 由g2+9 ,而t=()x是减函数. ∴要求g(x)的增区间实际上是求g(t)的减区间. 求g(x)的减区间实际上是求g(t)的增区间. ∵g(t)在(0.2]上递增.在[2.+∞)上递减. 由0<t=()x≤2,可得x≥-1, 由t=()x≥2,可得x≤-1. ∴g上递减.在(-∞.-1]上递增. 故g(x)的单调递增区间是(-∞.-1]. 单调递减区间是[-1.+∞). 例4 =是R上的偶函数. (1)求a的值, 上是增函数. 是R上的偶函数.∴f. 1分 ∴ ∴(a-)(ex-)=0对一切x均成立. 3分 ∴a-=0.而a>0,∴a=1. 4分 上任取x1.x2.且x1<x2, 5分 则f(x1)-f(x2)= 8分 ∵x1<x2,∴,有>0. ∵x1>0,x2>0,∴x1+x2>0,∴>1, 10分 -1<0.∴f(x1)-f(x2)<0, 即f(x1)<f(x2), 故f上是增函数. 12分
网址:http://m.1010jiajiao.com/timu_id_4463458[举报]
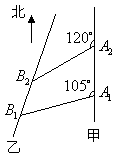
(2007山东理20)如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
(08年山东卷理)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为
(A)304.6 (B)303.6 (C)302.6 (D)301.6