摘要：10．数列{an}的前n项和Sn＝n2+1.数列{bn}满足:b1＝1.当n≥2时.bn＝abn-1.设数列{bn}的前n项和为Tn.则T2007＝ . 答案:22006+2006 解析:由题意得a1＝2.当n≥2时.an＝Sn-Sn-1＝(n2+1)-[(n-1)2+1]＝2n-1.由此可得.an≥2.当n≥2时.bn＝abn-1≥2.b2＝ab1＝a1＝2.当n≥2时bn＝abn-1≥2.当n≥3时.bn-1≥2.bn＝abn-1＝2bn-1-1.bn-1＝2(bn-1-1).bn-1＝2n-2(b2-1)＝2n-2.bn＝2n-2+1(n≥2).因此T2007＝1+2+(2+1)+(22+1)+-+(22005+1)＝(1+2+22+-+22005)+2007＝+2007＝22006+2006.

网址：http://m.1010jiajiao.com/timu_id_4462653[举报]
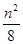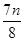
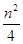