摘要:(二).研讨新知 一个直观的想法是:如果能够将零点所在的范围尽量的缩小.那么在一定的精确度的要求下.我们可以得到零点的近似值,为了方便.我们通过“取中点 的方法逐步缩小零点所在的范围. 取区间(2.3)的中点2.5.用计算器算得f(2.5)≈-0.084,因为f<0,所以零点在区间内, 再取区间的中点2.75.用计算器算得f≈0.512,因为f<0,所以零点在内, 由于.越来越小.所以零点所在范围确实越来越小了,重复上述步骤.那么零点所在范围会越来越小.这样在有限次重复相同的步骤后.在一定的精确度下.将所得到的零点所在区间上任意的一点作为零点的近似值.特别地可以将区间的端点作为零点的近似值.例如.当精确度为0.01时.由于∣2.5390625-2.53125∣=0.0078125<0.01.所以我们可以将x=2.54作为函数f(x)=㏑x+2x-6零点的近似值.也就是方程㏑x+2x-6=0近似值. 这种求零点近似值的方法叫做二分法. 1.师:引导学生仔细体会上边的这段文字.结合课本上的相关部分.感悟其中的思想方法. 生:认真理解二分法的函数思想.并根据课本上二分法的一般步骤.探索其求法. 2.为什么由︱a - b ︳<便可判断零点的近似值为a(或b)? 先由学生思考几分钟.然后作如下说明: 设函数零点为x0.则a<x0<b.则: 0<x0-a<b-a.a-b<x0-b<0, 由于︱a - b ︳<.所以 ︱x0 - a ︳<b-a<,︱x0 - b ︳<∣ a-b∣<, 即a或b 作为零点x0的近似值都达到了给定的精确度. ㈢.巩固深化.发展思维 1. 学生在老师引导启发下完成下面的例题 例2.借助计算器用二分法求方程2x+3x=7的近似解 问题:原方程的近似解和哪个函数的零点是等价的? 师:引导学生在方程右边的常数移到左边.把左边的式子令为f(x),则原方程的解就是f(x)的零点. 生:借助计算机或计算器画出函数的图象.结合图象确定零点所在的区间.然后利用二分法求解.
网址:http://m.1010jiajiao.com/timu_id_4460350[举报]
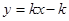 ,若y随x的增大而增大,则它的图象经过 ( )
,若y随x的增大而增大,则它的图象经过 ( ) (x>-1)的反函数的图象经过
(x>-1)的反函数的图象经过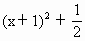 (x>-1)的反函数的图象经过
(x>-1)的反函数的图象经过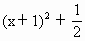 (x>-1)的反函数的图象经过
(x>-1)的反函数的图象经过