摘要:(二) 互动交流 研讨新知 函数零点的概念: 对于函数.把使成立的实数叫做函数的零点. 函数零点的意义: 函数的零点就是方程实数根.亦即函数的图象与轴交点的横坐标. 即: 方程有实数根函数的图象与轴有交点函数有零点. 函数零点的求法: 求函数的零点: ①求方程的实数根, ②对于不能用求根公式的方程.可以将它与函数的图象联系起来.并利用函数的性质找出零点. 1.师:引导学生仔细体会左边的这段文字.感悟其中的思想方法. 生:认真理解函数零点的意义.并根据函数零点的意义探索其求法: ①代数法, ②几何法. 2.根据函数零点的意义探索研究二次函数的零点情况.并进行交流.总结概括形成结论. 二次函数的零点: 二次函数 . (1)△>0.方程有两不等实根.二次函数的图象与轴有两个交点.二次函数有两个零点. (2)△=0.方程有两相等实根.二次函数的图象与轴有一个交点.二次函数有一个二重零点或二阶零点. (3)△<0.方程无实根.二次函数的图象与轴无交点.二次函数无零点. 3.零点存在性的探索: (Ⅰ)观察二次函数的图象: ① 在区间上有零点 , . , · 0. ② 在区间上有零点 , · 0. (Ⅱ)观察下面函数的图象 ① 在区间上 零点, · 0. ② 在区间上 零点, · 0. ③ 在区间上 零点, · 0. 由以上两步探索.你可以得出什么样的结论? 怎样利用函数零点存在性定理.断定函数在某给定区间上是否存在零点? 4.生:分析函数.按提示探索.完成解答.并认真思考. 师:引导学生结合函数图象.分析函数在区间端点上的函数值的符号情况.与函数零点是否存在之间的关系. 生:结合函数图象.思考.讨论.总结归纳得出函数零点存在的条件.并进行交流.评析. 师:引导学生理解函数零点存在定理.分析其中各条件的作用.
网址:http://m.1010jiajiao.com/timu_id_4460339[举报]
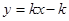 ,若y随x的增大而增大,则它的图象经过 ( )
,若y随x的增大而增大,则它的图象经过 ( )