摘要：重点:对数运算的性质与对数知识的应用 难点:正确使用对数的运算性质
网址：http://m.1010jiajiao.com/timu_id_4460264[举报]
对对数函数的图象和性质的研究，教材是根据互为反函数的图象特征，由指数函数的图象再作出其关于直线y＝x的图象，即得对数函数的图象，在数形结合的数学思想指导下，推得对数函数的性质．请归纳对数函数y＝logax(a＞0且a≠1)的性质．
对数的性质与运算法则（以下标中a＞0且a≠1，m、n＞0，b＞0且b≠1）
（1）①loga1= ②logaa= ③负数与零没有对数
（2）①logaMN= ． ②loga
= ． ③logambn= ．
（3）①aloga N= ． ②lg2+lg5= ．
查看习题详情和答案>>
（1）①loga1=
（2）①logaMN=
| M | N |
（3）①aloga N=
教科书中有如下的对数运算性质：loga（MN）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）．已知f（x）、g（x）互为反函数（x∈R），若函数g（x）有性质：对于任意的实数m，n，有g（mn）=g（m）+g（n），通过类比的思想，猜想函数f（x）性质：
查看习题详情和答案>>
对于任意的实数m，n，有f（m+n）=f（m）•f（n）
对于任意的实数m，n，有f（m+n）=f（m）•f（n）
．
)=(lgx)2+lgy+
B.lg(x2y
)=(lgx)2+lgy+2lgz
)=2lgx+lgy－2lgz D.lg(x2y
)=2lgx+lgy+
lgz
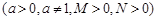．已知
、
互为反函数
，若函数
有性质：对于任意的实数
，有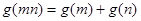
，通过类比的思想，猜想函数
性质：___________________________________________．