摘要:(二)研探新知 投影问题2:观察下面几个例子.你能发现两个集合间有什么关系了吗? (1), (2)设A为国兴中学高一(3)班男生的全体组成的集合.B为这个班学生的全体组成的集合, (3)设 (4). 组织学生充分讨论.交流.使学生发现两个集合所含元素范围存在各种关系.从而类比得出两个集合之间的关系: ①一般地.对于两个集合A.B.如果集合A中任意一个元素都是集合B中的元素.我们就说这两个集合有包含关系.称集合A为B的子集. 记作: 读作:A含于B. ②如果两个集合所含的元素完全相同.那么我们称这两个集合相等. 教师引导学生类比表示集合间关系的符号与表示两个实数大小关系的等号之间有什么类似之处.强化学生对符号所表示意义的理解.并指出:为了直观地表示集合间的关系.我们常用平面上封闭曲线的内部代表集合.这种图称为Venn图.如图l和图2分别是表示问题2中实例1和实例3的Venn图. 图1 图2 投影问题3:与实数中的结论“若 相类比.在集合中.你能得出什么结论? 教师引导学生通过类比.思考得出结论: 若. 问题4:请同学们举出几个具有包含关系.相等关系的集合实例.并用Venn图表示. 学生主动发言.教师给予评价.
网址:http://m.1010jiajiao.com/timu_id_4460095[举报]
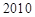 年
年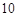 月
月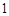 日
日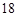 时
时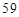 分
分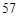 秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约
秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约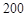 公里、远地点高度约
公里、远地点高度约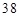 万公里的直接奔月椭圆(地球球心
万公里的直接奔月椭圆(地球球心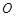 为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面
为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面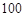 公里、近月面
公里、近月面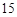 公里(月球球心
公里(月球球心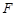 为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以
为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以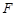 为圆心、距月面
为圆心、距月面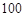 公里的圆形轨道Ⅲ绕月飞行,并开展相关技术试验和科学探测。已知地球半径约为
公里的圆形轨道Ⅲ绕月飞行,并开展相关技术试验和科学探测。已知地球半径约为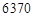 公里,月球半径约为
公里,月球半径约为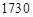 公里。
公里。
(Ⅰ)比较椭圆轨道Ⅰ与椭圆轨道Ⅱ的离心率的大小;
(Ⅱ)以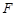 为右焦点,求椭圆轨道Ⅱ的标准方程。
为右焦点,求椭圆轨道Ⅱ的标准方程。
查看习题详情和答案>>
如图所示,2010年10月1日“嫦娥二号”探月卫星沿地月转移轨道飞向月球,在月球附近一点![]() 变轨进入以月球球心
变轨进入以月球球心![]() 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在![]() 点第二次变轨进入仍以
点第二次变轨进入仍以![]() 为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在
为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在![]() 点第三次变轨进入以
点第三次变轨进入以![]() 为圆心的圆形轨道Ⅲ绕月飞行,若用
为圆心的圆形轨道Ⅲ绕月飞行,若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①![]() ; ②
; ②![]() ;
;
 ③
③![]() ; ④
; ④![]() <
<![]() .
.
其中正确式子的序号是 ▲ .
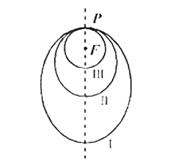
查看习题详情和答案>>如图所示,2010年10月1日“嫦娥二号”探月卫星沿地月转移轨道飞向月球,在月球附近一点![]() 变轨进入以月球球心
变轨进入以月球球心![]() 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在![]() 点第二次变轨进入仍以
点第二次变轨进入仍以![]() 为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在
为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在![]() 点第三次变轨进入以
点第三次变轨进入以![]() 为圆心的圆形轨道Ⅲ绕月飞行,若用
为圆心的圆形轨道Ⅲ绕月飞行,若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①![]() ; ②
; ②![]() ;
;
 ③
③![]() ; ④
; ④![]() <
<![]() .
.
其中正确式子的序号是 ▲ .
查看习题详情和答案>>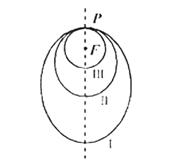 ①
①