摘要:24.(1)当a=0时.0<0不成立.原不等式的解集为Ф, 当a<0时.不等式的解集也为Ф,当a>0时.不等式即|x|<1.∴解集为{x|-1<x<1}. x≤b+2. 10当a>1时.a-1>0.∴此时不等式的解集为{x|x≤}. 20当a<1时.a-1<0.∴此时不等式的解集为{x|x≥}. 30当a=1时.a-1=0.若b≥-2.则不等式的解集为实数集R. 若b<-2.则不等式的解集为Ф.
网址:http://m.1010jiajiao.com/timu_id_4460019[举报]
(本小题满分14分)
已知函数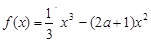
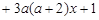 ,a∈R.
,a∈R.
(1)当a=0时,求曲线y=f(x)在点(3,f(3))处的切线方程:
(2)当函数y=f'(x)在(0,4)上有唯一的零点时,求实数a的取值范围.
查看习题详情和答案>>
设f(x)=
(a为实常数),y=g(x)与y=e-x的图象关于y轴对称.
(1)若函数y=f[g(x)]为奇函数,求a的取值.
(2)当a=0时,若关于x的方程f[g(x)]=
有两个不等实根,求m的范围;
(3)当|a|<1时,求方程f(x)=g(x)的实数根个数,并加以证明.
查看习题详情和答案>>
| 2-x+a |
| 1+x |
(1)若函数y=f[g(x)]为奇函数,求a的取值.
(2)当a=0时,若关于x的方程f[g(x)]=
| g(x) |
| m |
(3)当|a|<1时,求方程f(x)=g(x)的实数根个数,并加以证明.
已知函数f(x)=ln(1+xx)-ax,其中a>0
(1)求函数f(x)的单调区间;
(2)如果a∈(0,1),当a≥0时,不等式f(x)-m<0的解集为空集,求实数m的取值范围;
(3)当x>1时,若g(x)=f[ln(x-1)]+aln(x-1),试证明:对n∈N*,当n≥2时,有g(
)>-
.
查看习题详情和答案>>
(1)求函数f(x)的单调区间;
(2)如果a∈(0,1),当a≥0时,不等式f(x)-m<0的解集为空集,求实数m的取值范围;
(3)当x>1时,若g(x)=f[ln(x-1)]+aln(x-1),试证明:对n∈N*,当n≥2时,有g(
| 1 |
| n! |
| n(n-1) |
| 2 |