摘要:25.如题25图.离子源A产生的初速为零.带电量均为e.质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管.垂直射入匀强偏转电场.偏转后通过极板HM上的小孔S离开电场.经过一段匀速直线运动.垂直于边界MN进入磁感应强度为B的匀强磁场.已知HO=d.HS=2d.=90°. (1)求偏转电场场强E0的大小以及HM与MN的夹角φ, (2)求质量为m的离子在磁场中做圆周运动的半径, (3)若质量为4m的离子垂直打在NQ的中点S1处.质量为16m的离子打在S2处.求S1和S2之间的距离以及能打在NQ上的正离子的质量范围. 解析:(1)正离子被电压为U0的加速电场加速后速度设为v1.设 对正离子.应用动能定理有eU0=mv12. 正离子垂直射入匀强偏转电场.作类平抛运动 受到电场力F=qE0.产生的加速度为a=. 即a=. 垂直电场方向匀速运动.有2d=v1t. 沿场强方向:Y=at2. 联立解得E0= 又tanφ=.解得φ=45°, (2)正离子进入磁场时的速度大小为v2=. 正离子在匀强磁场中作匀速圆周运动.由洛仑兹力提供向心力 qv2B=. 解得离子在磁场中做圆周运动的半径R=2, (3)根据R=2可知. 质量为4m的离子在磁场中的运动打在S1.运动半径为R1=2. 质量为16m的离子在磁场中的运动打在S2.运动半径为R2=2. 又ON=R2-R1. 由几何关系可知S1和S2之间的距离ΔS=-R1. 联立解得ΔS=4(-1), 由R′2=(2 R1)2+( R′-R1)2解得R′=R1. 再根据R1<R<R1. 解得m<mx<25m.
网址:http://m.1010jiajiao.com/timu_id_4455730[举报]
(2009年高考重庆理综卷)密闭有空气的薄塑料瓶因降温而变扁,此过程中瓶内空气(不计分子势能)( )
A.内能增大,放出热量 B.内能减小,吸收热量
C.内能增大,对外界做功 D.内能减小,外界对其做功
查看习题详情和答案>>
(2009年高考重庆卷)某科学家提出年轻热星体中核聚变的一种理论,其中的两个核反应方程为
 H+
H+ C―→
C―→ N+Q1
N+Q1  H+
H+ N―→
N―→ C+X+Q2
C+X+Q2
方程中Q1、Q2表示释放的能量,相关的原子核质量见下表:

以下推断正确的是( )
A.X是 He,Q2>Q1 B.X是
He,Q2>Q1 B.X是 He,Q2>Q1
He,Q2>Q1
C.X是 He,Q2<Q1 D.X是
He,Q2<Q1 D.X是 He,Q2<Q1
He,Q2<Q1
查看习题详情和答案>>
(2009年高考重庆卷)某科学家提出年轻热星体中核聚变的一种理论,其中的两个核反应方程为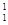 H+
H+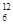 C―→
C―→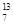 N+Q1
N+Q1 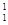 H+
H+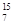 N―→
N―→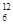 C+X+Q2
C+X+Q2
方程中Q1、Q2表示释放的能量,相关的原子核质量见下表: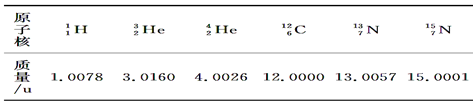
以下推断正确的是( )
A.X是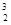 He,Q2>Q1 He,Q2>Q1 | B.X是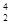 He,Q2>Q1 He,Q2>Q1 |
C.X是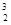 He,Q2<Q1 He,Q2<Q1 | D.X是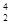 He,Q2<Q1 He,Q2<Q1 |
(2009年高考重庆理综卷)密闭有空气的薄塑料瓶因降温而变扁,此过程中瓶内空气(不计分子势能)( )
| A.内能增大,放出热量 | B.内能减小,吸收热量 |
| C.内能增大,对外界做功 | D.内能减小,外界对其做功 |