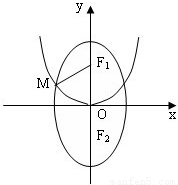
摘要：◆教师:制作点P的动画.并追踪点P得到点P的轨迹如图1.根据屏幕中的动画.请说出其意义. 学生A:点P的轨迹是一个圆. 学生B:动点P到定点A的距离等于定值6.故由圆的定义.动点P的轨迹是以点A为圆心.以6为半径的圆. 教师:两位同学回答得都很好.但第二位同学把他所得出结论的理由说得非常清楚.我们再看下一个动画: ◆教师:根据屏幕中的动画.请你用准确语言描述此动画是什么意思?通过什么数学方法验证你的上述判断? 学生C:动点P的轨迹似乎是一个圆. 学生D:动点Q在定圆O上运动.点A是一定点.动点P满足.我的判断也是动点P的轨迹是一个圆. 教师:第一位同学回答中说到了“似乎 .这实际上是通过信息技术的优势得出的一个直觉判断.在数学乃至所有自然科学中.直觉判断确实是发现真理的有效方法.第二位同学观察得较为细致.表达的语言也非常流畅,两位同学的最后判断都说动点P的轨迹是圆.究竟是不是呢?有哪一位同学上来给出文字的论证? 学生D上来在黑板写下了他的文字论证: 不妨设定圆O的方程为:.定点.点Q的圆O点的动点. 又设动点.., 由 把代入圆O方程. 即得点P的轨迹方程:.此方程表示以点为圆心.以2为半径的圆.
网址：http://m.1010jiajiao.com/timu_id_4450270[举报]
如图，已知F1、F2分别为椭圆C1：| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| 3 |
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
| AP |
| PB |
| AQ |
| QB |
求证：点Q总在某条定直线上．
已知抛物线的顶点在坐标原点，焦点为F（1，0），点P是点F关于y轴的对称点，过点P的动直线ι交抛物线与A，B两点．
（1）若△AOB的面积为
，求直线ι的斜率；
（2）试问在x轴上是否存在不同于点P的一点T，使得TA，TB与x轴所在的直线所成的锐角相等，若存在求出定点T的坐标，若不存在说明理由．
查看习题详情和答案>>
（1）若△AOB的面积为
| 5 | 2 |
（2）试问在x轴上是否存在不同于点P的一点T，使得TA，TB与x轴所在的直线所成的锐角相等，若存在求出定点T的坐标，若不存在说明理由．
与向量、圆交汇．例5：已知F1、F2分别为椭圆C1：| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| 3 |
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
| AP |
| PB |
| AQ |
| QB |
、
分别为椭圆
：
的 
：
的焦点，
是
。
：
，过点P的动直线
与圆
，
（
且
）。求证：点Q总在某定直线上。
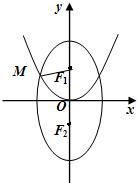
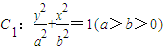的上、下焦点，其中F1也是抛物线
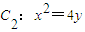的焦点，点M是C1与C2在第二象限的交点，且
．
，
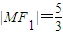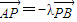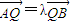（λ≠0且λ≠±1），