摘要：3．关于叶肉细胞在光照条件下产生ATP的描述.正确的是( ) A．无氧条件下.光合作用是细胞ATP的唯一来源 B．有氧条件下.线粒体.叶绿体和细胞质基质都能产生ATP C．线粒体和叶绿体合成ATP都依赖氧 D．细胞质中消耗的ATP均来源于线粒体和叶绿体
网址：http://m.1010jiajiao.com/timu_id_4448126[举报]
（2012•黄浦区二模）对n∈N*，定义函数fn（x）=-（x-n）2+n，n-1≤x≤n．
（1）求证：y=fn（x）图象的右端点与y=fn+1（x）图象的左端点重合；并回答这些端点在哪条直线上．
（2）若直线y=knx与函数fn（x）=-（x-n）2+n，n-1≤x≤n（n≥2，n∈N*）的图象有且仅有一个公共点，试将kn表示成n的函数．
（3）对n∈N*，n≥2，在区间[0，n]上定义函数y=f（x），使得当m-1≤x≤m（n∈N*，且m=1，2，…，n）时，f（x）=fm（x）．试研究关于x的方程f（x）=fn（x）（0≤x≤n，n∈N*）的实数解的个数（这里的kn是（2）中的kn），并证明你的结论．
查看习题详情和答案>>
（1）求证：y=fn（x）图象的右端点与y=fn+1（x）图象的左端点重合；并回答这些端点在哪条直线上．
（2）若直线y=knx与函数fn（x）=-（x-n）2+n，n-1≤x≤n（n≥2，n∈N*）的图象有且仅有一个公共点，试将kn表示成n的函数．
（3）对n∈N*，n≥2，在区间[0，n]上定义函数y=f（x），使得当m-1≤x≤m（n∈N*，且m=1，2，…，n）时，f（x）=fm（x）．试研究关于x的方程f（x）=fn（x）（0≤x≤n，n∈N*）的实数解的个数（这里的kn是（2）中的kn），并证明你的结论．
关于方程x2+2y2-ax+ay-a-1=0（a∈R）表示的椭圆，给出以下四个命题：①椭圆的中心在一条直线上运动；②椭圆的大小不变；③不论a取什么值，椭圆总过两个定点；④椭圆的离心率不变．其中错误命题的个数是 ．
查看习题详情和答案>>
如图，在直角坐标系xOy中，△AiBiAi+1（i=1，2，…，n，…）为正三角形，A1(-| 1 |
| 4 |
（1）求证：点B1，B2，…，Bn，…在同一条抛物线上，并求该抛物线C的方程；
（2）设直线l过坐标原点O，点B1关于l的对称点B′在y轴上，求直线l的方程；
（3）直线m过（1）中抛物线C的焦点F并交C于M、N，若
| MF |
| FN |
| EF |
| EM |
| EN |
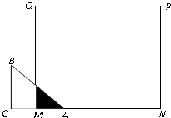已知如图，等腰三角形ABC的直角边长为a，正方形MNPQ的边为b （a＜b），C、M、A、N在同一条直线上，开始时点A与点M重合，让△ABC向右移动，最后点C与点N重合．设三角形与正方形的重合面积为y，点A移动的距离为x，则y关于x的大致图象是（ ）
查看习题详情和答案>>
医学上为研究传染病传播中病毒细胞的发展规律及其预防，将病毒细胞注入一只小白鼠体内进行实验，经检测，病毒细胞的总数与天数的关系记录如下表．
已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡．但注射某种药物，将可杀死其体内该病毒细胞的97%．
（1）根据表格提供的数据，写出N关于t的函数解析式．
（2）为了使小白鼠在实验过程中不死亡，第一次最迟应在何时注射该种药物？
（3）按（1）中的结论，第二次最迟应在何时注射该种药物，才能维持小白鼠的生命？（精确到天，参考数据：lg3=0.3010．）
查看习题详情和答案>>
| 天数t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 病毒细胞总数N | 1 | 3 | 9 | 27 | 81 | 243 | 729 | … |
（1）根据表格提供的数据，写出N关于t的函数解析式．
（2）为了使小白鼠在实验过程中不死亡，第一次最迟应在何时注射该种药物？
（3）按（1）中的结论，第二次最迟应在何时注射该种药物，才能维持小白鼠的生命？（精确到天，参考数据：lg3=0.3010．）