摘要： 如图.已知直线l:y=kx+2.k＜0 .与y轴交于点A.与x轴交于点B.以OA为直径的⊙P交l于另一点D.把弧AD沿直线l翻转后与OA交于点E. (1)当k=-2时.求OE的长(4)分 (2)是否存在实数k.k＜0 .使沿直线l把弧AD翻转后所得的弧与OA相切? 若存在.请求出此时k的值.若不存在.请说明理由.(6)分 [命题意图]圆在坐标系的变换情况 [参考答案]答案:如图所示.由 ∠DEO=∠EAD+∠ADE= =∠AOD 所以.OD=DE 当k=-2时.易得A.OA=2.OB=1.则AB= 因为BO与⊙P切于点O.由切割线定理.得 OB2=BD·ABBD= 过点D作DC⊥AO于点C.则 OE=2OC.DC∥OB 从而.有 故OE= (4) (2)假设存在实数k使得弧AD沿直线l翻转后所得弧与OA相切.则切点必为A.即E与A重合.由(1)知OD=AD. 又∠ADO=90°.所以 ∠OAD=45° 此时.OB=OA=2.B(2.0) ∴k=-1. 故存在k=-1.使得弧AD沿直l翻转后所得弧与OA相切. (6) [试题来源]2009北京中考模拟
网址：http://m.1010jiajiao.com/timu_id_4443090[举报]
如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线y2=
（x＜0）分别交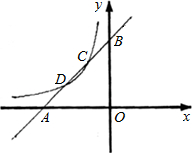
于点C、D，且C点的坐标为（-1，2）．
（1）分别求出直线AB及双曲线的解析式；
（2）求出点D的坐标；
（3）利用图象直接写出：当在什么范围内取值时，y1＞y2；
（4）在坐标轴上找一点M，使得以M、C、D为顶点的三角形是等腰三角形，请写出M的坐标． 查看习题详情和答案>>
| k | x |
于点C、D，且C点的坐标为（-1，2）．（1）分别求出直线AB及双曲线的解析式；
（2）求出点D的坐标；
（3）利用图象直接写出：当在什么范围内取值时，y1＞y2；
（4）在坐标轴上找一点M，使得以M、C、D为顶点的三角形是等腰三角形，请写出M的坐标． 查看习题详情和答案>>
如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线y2=
（x＜0）分别交于点
C、D，且C点的坐标为（-1，2）．
（1）分别求出直线AB及双曲线的解析式；
（2）求出点D的坐标；
（3）利用图象直接写出：当x在什么范围内取值时，y1＞y2？ 查看习题详情和答案>>
| k | x |
C、D，且C点的坐标为（-1，2）．（1）分别求出直线AB及双曲线的解析式；
（2）求出点D的坐标；
（3）利用图象直接写出：当x在什么范围内取值时，y1＞y2？ 查看习题详情和答案>>
如图，在Rt△OAB中，∠OBA=90°，点B在x轴上，点A在第二象限，已知双曲线y=| k | x |
（-3，2）
（-3，2）
；（2）△AOC的面积为9
9
．
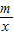的图象的两个交点．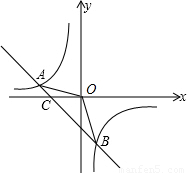
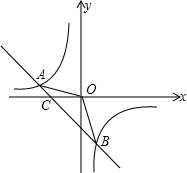如图：已知A（-4，n）、B（2，-4）是一次函数y1=kx+b的图象与反比例函数y2=
的图象的两个交点．