摘要:例1 1°用反三角函数表示中的角x 2°用反三角函数表示中的角x 解:1° ∵ ∴ 又由 得 ∴ ∴ 2° ∵ ∴ 又由 得 ∴ ∴ 例2 已知.求角x的集合 解:∵ ∴ 由 得 由 得 故角x的集合为 例3 求的值 解:arctan2 = a, arctan3 = b 则tana = 2. tanb = 3 且. ∴ 而 ∴a + b = 又arctan1 = ∴= p 例4求y = arccos(sinx), ()的值域 解:设u = sin x ∵ ∴ ∴ ∴所求函数的值域为 例5设xÎ[0,], f (x)=sin, g (x)=cos 求f (x)和g (x)的最大值和最小值.并将它们按大小顺序排列起来 解:∵在[0,]上y=cosx单调递减, 且cosxÎ[0,1] 在此区间内y=sinx单调递增且sinxÎ[0,1] ∴f (x)=sinÎ[0,sin1] 最小值为0, 最大值为sin1 g (x)=cosÎ[cos1,1] 最小值为cos1, 最大值为1 ∵cos1=sin(-1)<sin1 ∴它们的顺序为:0<cos1<sin1<1 例6 已知△ABC的两边a, b .它们的夹角为C 1°试写出△ABC面积的表达式, 2°当ÐC变化时.求△AABC面积的最大值 解:1° 如图:设AC边上的高h=asinC 2°当C=90°时[sinC]max=1 ∴[S△ABC]max= 例7 求函数的最大值和最小值 解: 当cosx=1时 ymax=,当cosx=-1时 ymin= -2 例8求函数 (≤x≤)的最大值和最小值 解:∵xÎ[,] ∴x-Î[-,] ∴当x-=0 即x=时 ymax=2 当x-= 即x=时 ymin=1 例9求函数f (x)=的单调递增区间 解:∵f (x)= 令 ∴y= .t是x的增函数 又∵0<<1 ∴当y=为单调递增时 cost为单调递减 且cost>0 ∴2kp≤t<2kp+ ∴2kp≤<2kp+ 6kp-≤x<6kp+ ∴f (x)=的单调递减区间是[6kp-,6kp+)
网址:http://m.1010jiajiao.com/timu_id_4441894[举报]
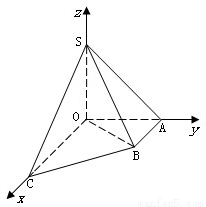
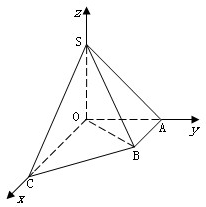 如图直角梯形OABC中,∠COA=∠OAB=
如图直角梯形OABC中,∠COA=∠OAB=| π |
| 2 |
(1)求
| SC |
| OB |
(2)设
| n |
| n |
①
| n |
②OA与平面SBC的夹角β(用反三角函数表示);
③O到平面SBC的距离.
(3)设
| k |
| k |
| SC |
| k |
| OB |
①
| k |
②异面直线SC、OB的距离为
如图直角梯形OABC中,∠COA=∠OAB=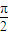 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(1)求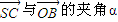 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(2)设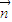 =(1,p,q),满足
=(1,p,q),满足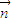 ⊥平面SBC,求:
⊥平面SBC,求:
①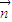 的坐标;
的坐标;
②OA与平面SBC的夹角β(用反三角函数表示);
③O到平面SBC的距离.
(3)设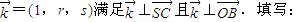
①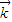 的坐标为______.
的坐标为______.
②异面直线SC、OB的距离为______
 查看习题详情和答案>>
查看习题详情和答案>>
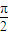 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.(1)求
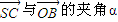 的大小(用反三角函数表示);
的大小(用反三角函数表示);(2)设
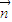 =(1,p,q),满足
=(1,p,q),满足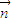 ⊥平面SBC,求:
⊥平面SBC,求:①
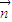 的坐标;
的坐标;②OA与平面SBC的夹角β(用反三角函数表示);
③O到平面SBC的距离.
(3)设
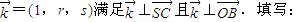
①
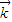 的坐标为______.
的坐标为______.②异面直线SC、OB的距离为______
 查看习题详情和答案>>
查看习题详情和答案>>
 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz. 的大小(用反三角函数表示);
的大小(用反三角函数表示); =(1,p,q),满足
=(1,p,q),满足 ⊥平面SBC,求:
⊥平面SBC,求: 的坐标;
的坐标;
 的坐标为______.
的坐标为______.
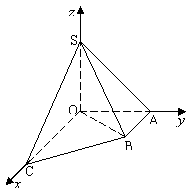 (本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=
(本题满分16分)如图直角梯形OABC中,∠COA=∠OAB=