摘要:∵.则点到两点的距离之积为.
网址:http://m.1010jiajiao.com/timu_id_444030[举报]
附加题:
设不等式组 表示的平面区域为D,区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为2。
表示的平面区域为D,区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为2。
(1)记点P的轨迹为曲线C,则曲线C的方程为_______;
(2)在(1)的前提下,若过点 ,斜率是k的直线l与曲线C交于A、B两点,记|AB|=f(x),则线段AB的长f(x)=_______;
,斜率是k的直线l与曲线C交于A、B两点,记|AB|=f(x),则线段AB的长f(x)=_______;
(3)在(2)的前提下,若以线段AB为直径的圆与y轴相切,则直线l的斜率k的值为_______。
查看习题详情和答案>>
设不等式组
 表示的平面区域为D,区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为2。
表示的平面区域为D,区域D内的动点P到直线x+y=0和直线x-y=0的距离之积为2。 (1)记点P的轨迹为曲线C,则曲线C的方程为_______;
(2)在(1)的前提下,若过点
 ,斜率是k的直线l与曲线C交于A、B两点,记|AB|=f(x),则线段AB的长f(x)=_______;
,斜率是k的直线l与曲线C交于A、B两点,记|AB|=f(x),则线段AB的长f(x)=_______; (3)在(2)的前提下,若以线段AB为直径的圆与y轴相切,则直线l的斜率k的值为_______。
如图,在梯形ABCD中,AB∥DC,AB=a,CD=b(a>b).若EF∥AB,EF到CD与AB的距离之比为m:n,则可推算出: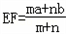 .试用类比的方法,推想出下述问题的结果.在上面的梯形AB∥CD中,延长梯形两腰 AD,BC相交于O点,设△OAB,△OCD的面积分别为S1,S2,EF∥AB且EF到CD与AB的距离之比为m:n,则△OEF的面积S0与S1,S2的关系是( )。
.试用类比的方法,推想出下述问题的结果.在上面的梯形AB∥CD中,延长梯形两腰 AD,BC相交于O点,设△OAB,△OCD的面积分别为S1,S2,EF∥AB且EF到CD与AB的距离之比为m:n,则△OEF的面积S0与S1,S2的关系是( )。
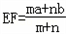 .试用类比的方法,推想出下述问题的结果.在上面的梯形AB∥CD中,延长梯形两腰 AD,BC相交于O点,设△OAB,△OCD的面积分别为S1,S2,EF∥AB且EF到CD与AB的距离之比为m:n,则△OEF的面积S0与S1,S2的关系是( )。
.试用类比的方法,推想出下述问题的结果.在上面的梯形AB∥CD中,延长梯形两腰 AD,BC相交于O点,设△OAB,△OCD的面积分别为S1,S2,EF∥AB且EF到CD与AB的距离之比为m:n,则△OEF的面积S0与S1,S2的关系是( )。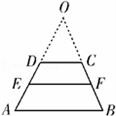
选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题。如果多做,则按所做的第一题计分。)
22.选修4-1:几何证明选讲
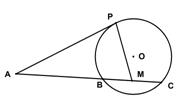
如图,已知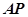 是⊙
是⊙ 的切线,
的切线,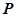 为切点,
为切点,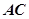 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于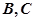 两点,圆心
两点,圆心 在
在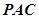 的内部,点
的内部,点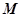 是
是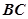 的中点。
的中点。
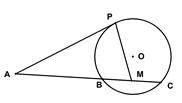
(1)证明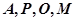 四点共圆;
四点共圆;
(2)求 的大小。
的大小。
23.选修4—4:坐标系与参数方程[来源:ZXXK]
已知直线 经过点
经过点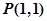 ,倾斜角
,倾斜角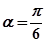 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与曲线
与曲线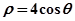 相交于两点
相交于两点 ,求点
,求点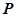 到
到 两点的距离之积。
两点的距离之积。
24.选修4—5:不等式证明选讲
若不等式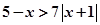 与不等式
与不等式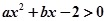 同解,而
同解,而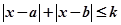 的解集为空集,求实数
的解集为空集,求实数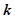 的取值范围。
的取值范围。
查看习题详情和答案>>
选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题。如果多做,则按所做的第一题计分。)
22.选修4-1:几何证明选讲
如图,已知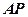 是⊙
是⊙ 的切线,
的切线,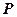 为切点,
为切点,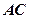 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于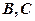 两点,圆心
两点,圆心 在
在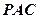 的内部,点
的内部,点
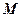 是
是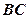 的中点。
的中点。
(1)证明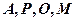 四点共圆;
四点共圆;
(2)求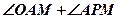 的大小。
的大小。
23.选修4—4:坐标系与参数方程
已知直线 经过点
经过点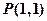 ,倾斜角
,倾斜角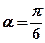 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与曲线
与曲线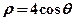 相交于两点
相交于两点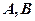 ,求点
,求点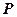 到
到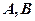 两点的距离之积。
两点的距离之积。
24.选修4—5:不等式证明选讲
若不等式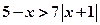 与不等式
与不等式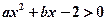 同解,而
同解,而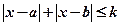 的解集为空集,求实数
的解集为空集,求实数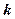 的取值范围。
的取值范围。
22.选修4-1:几何证明选讲
如图,已知
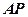 是⊙
是⊙ 的切线,
的切线,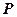 为切点,
为切点,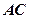 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于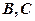 两点,圆心
两点,圆心 在
在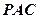 的内部,点
的内部,点
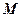 是
是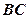 的中点。
的中点。
(1)证明
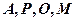 四点共圆;
四点共圆;(2)求
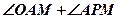 的大小。
的大小。23.选修4—4:坐标系与参数方程
已知直线
 经过点
经过点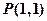 ,倾斜角
,倾斜角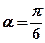 。
。(1)写出直线
 的参数方程;
的参数方程;(2)设
 与曲线
与曲线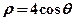 相交于两点
相交于两点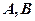 ,求点
,求点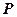 到
到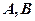 两点的距离之积。
两点的距离之积。24.选修4—5:不等式证明选讲
若不等式
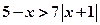 与不等式
与不等式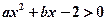 同解,而
同解,而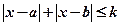 的解集为空集,求实数
的解集为空集,求实数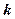 的取值范围。
的取值范围。 ,若l与圆x2+y2=4相交于A,B 两点,则点P到A,B两点的距离之积为( );弦|AB|=( )。
,若l与圆x2+y2=4相交于A,B 两点,则点P到A,B两点的距离之积为( );弦|AB|=( )。