在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+π),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加——青夏教育精英家教网—

摘要：在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+π),式中k=1 m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5 m/s的初速度沿杆向下运动,取重力加速度g=10 m/s2..则当小环运动到x= m时的速度大小v= m/s;该小环在x轴方向最远能运动到x= m处. 答案解析当x=0时,y1=2.5 cos π=-1.25 m,当x=时,y2=2.5 cos π=-2.5 m,由此可知,小环下落的高度为Δy=y1-y2=-1.25 m- m=1.25 m由动能定理得:mgΔy=mv2-mv02,代入数值得:v= m/s.当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0-mv02,则h==1.25 m,故当y=0时,小环速度为零,所以有2.5cos (kx+π)=0,得x=π

网址：http://m.1010jiajiao.com/timu_id_4440170[举报]

（07上海）物体沿直线运动的v－t关系如图所示，已知在第1 s内合外力对物体做的功为W，则

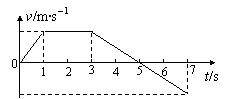A．从第1 s末到第3 s末合外力做功为4W